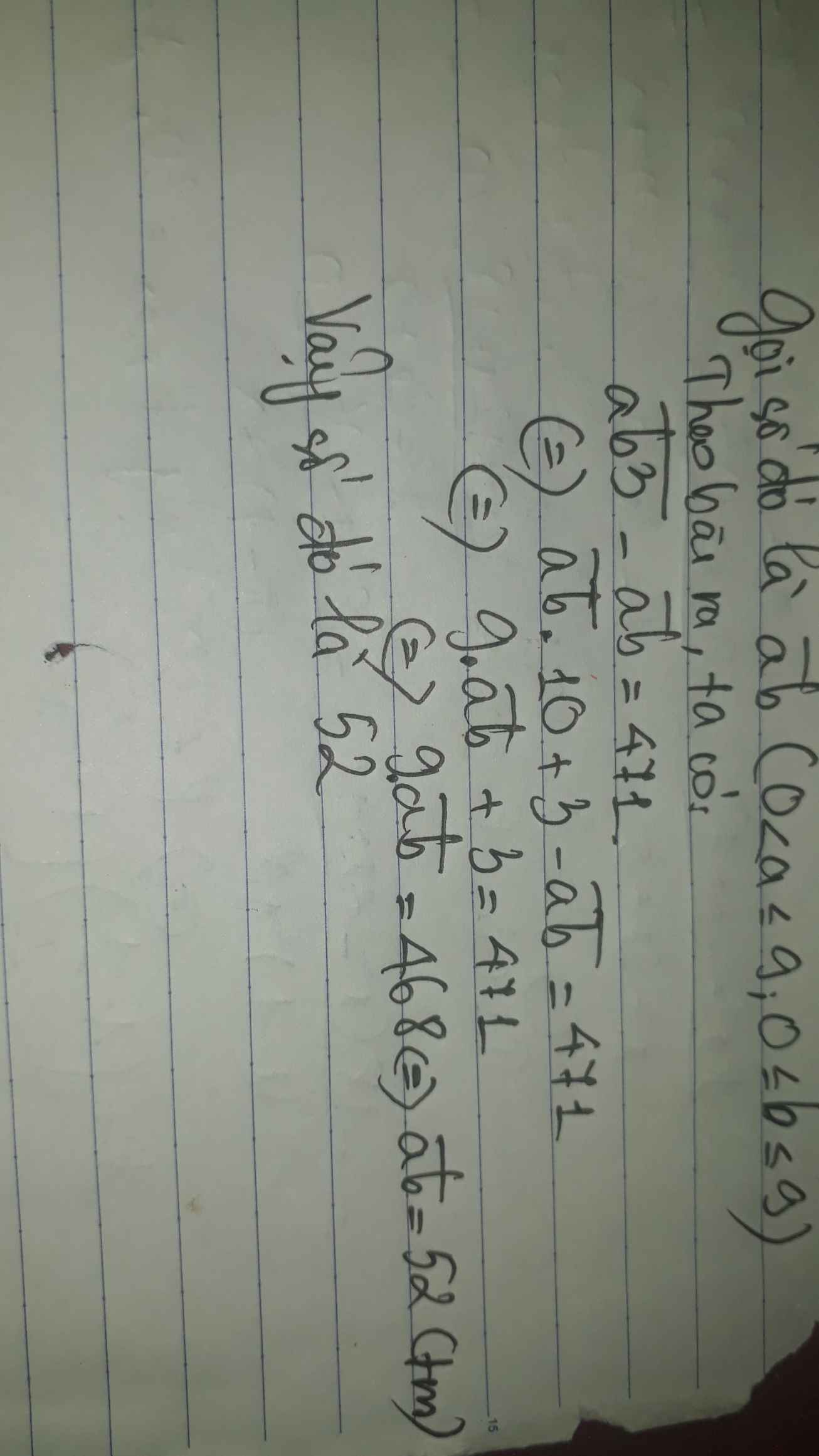a,

Gọi số cần tìm là ab

=> ab = 3b

=> 10a + b = 3b

=> 10a = 2b

=> 5a = b

=> b \(⋮\)5 ; b là chữ số nên có 1 chữ số

=> b = 5; a = 1

Vậy ab = 15

b, 

CÁCH 1:

Gọi số cần tìm là ab

=> ab3 = ab + 93

=> 100a + 10b + 3 = 10a + b + 93

=> 90a + 9b = 90

Mà a,b có 1 chữ số; a\(\ne0\)

Nếu a > 1 => 90a + 9b = 180 + 9b > 90 [loại]

=> a = 1 => b = 0

Vậy ab = 10

CÁCH 2:

Khi ta thêm số 3 vào bên phải một số thì số đó tăng 9 lần và 3 đơn vị.

Vậy số ban đầu là:

[93 - 3]: 9 = 10

c, 

CÁCH 1:

Gọi số cần tìm là ab

=> ab4 = ab + 112

=> 100a + 10b + 4 = 10a + b + 112

=> 90a + 9b = 108

Mà a,b có 1 chữ số; a\(\ne0\)

=> nếu a > 1 => 90a + 9b = 180 + 9b > 108 [loại]

=> a = 1 => b = [108 - 90.1]: 9 = 2

Vậy ab = 12

CÁCH 2 TƯƠNG TỰ BÀI TRÊN

Thanks nha!

Gọi số phải tìm là  ab\(a\ne0;a,b< 10\)

Theo đề bài ta có :

ab5 = ab + 230

10 . ab + 5 = ab + 230

9 . ab = 225

     ab  = 225 : 9

      ab = 25 

b,

Khi viết thêm chữ số 3 vào bên phải số tự nhiên có nghĩa là ta lấy số đó gấp lên 10 lần

=> Số cũ hơn số mới là 9 lần và 3 đơn vị.

=> Số cũ là :

                   ( 273 - 3 ) : 9 = 30 

                       Đáp số : 30

c,

khi viết thêm chữ số 2 vào bên phải số tự nhiên thì số đó tăng thêm 10 lần cộng với 2 đơn vị.

Vậy 4106 = 9 lần số đó + 2

Số đó là : (4106 - 2 ) : 9 = 456

                                Đáp số : 456

d,

Gọi số cần tìm là A
Ta có:
A6 = 10A + 6
<=> A6 - A = 10A + 6 - A = 3228
<=> 9A = 3228 - 6 = 3222
<=> A = 3222 : 9 = 358
Vậy số cần tìm là 358

Bn nhớ gạch đầu hộ mk .

a) Gọi số cần tìm là ab ( a ; b là chữ số , a khác 0 )

Theo đề ta có :

     ab5 - ab = 230

ab x 10 + 5 - ab = 230

( ab x 10 - ab ) + 5 = 230

ab x 9 + 5 = 230

ab x 9 = 230 - 5 = 225

ab = 225 : 9 = 25 ( thỏa mãn )

Vậy số cần tìm là 25

b) Khi viết thêm chữ số 3 vào bên phải một số tự nhiên tức là số đó gấp lên 10 lần và thêm 3 đơn vị hoặc tăng lên 9 lần bản thân nó và 3 đơn vị

=> Số cũ gấp số mới 9 lần và 3 đơn vị.

=> Số đó là :

     ( 273 - 3 ) : 9 = 30

Vậy số cần tìm là 30

c) Gọi số cần tìm là abc ( a ; b ; c là chữ số , a khác 0 )

Khi viết thêm chữ số 2 vào bên phải số đó ta được số abc2

Theo đề ta có :

abc2 - abc = 4106

10abc + 2 - abc = 4106

9abc = 4104

=> abc = 4104 : 9 = 456

Vậy số cần tìm là 456

d) Khi viết thêm chữ số 6 vào bên phải số đó thì tức là số đó gấp lên 10 lần và 6 đơn vị hoặc tăng lên 9 lần bản thân nó và 6 đơn vị

9 lần số đó là :

     3228 - 6 = 3222

Số đó là :

     3222 : 9 = 358

Vậy số cần tìm là 358

a) Gọi số cần tìm là ab (a ; b là chữ số, a khác 0)

Theo đề ta có:

      ab5 - ab = 230

ab x 10 + 5 - ab = 230

(ab x 10 - ab) + 5 = 230

ab x 9 + 5 =230

ab x 9 = 230 - 5 = 225

ab = 225 : 9 = 25 (thoả mãn)

Vậy số cần tìm là 25.

b) Khi viết thêm chữ số 3 vào bên phải một số tự nhiên Tức là số đó gấp lên 10 lần và thêm 3 đơn vị và tăng lên 9 lần bản thân nó và 3 đơn vị.
=> Số cuối gấp số mới 9 lần và 3 đơn vị.
=> Số đó là: (273 - 3) : 9 = 30
 Vậy số cần tìm là: 30.

c) Gọi số cần tìm là abc (a ; b ; c là chữ số, a khác 0)

Khi viết thêm chữ số 2 vào bên phải số đó được số abc2.

Theo đề ta có:

abc 2 - abc = 4106 
10 abc + 2 - abc = 4106 
9 abc = 4104
=> abc = 4104 chia 9 = 456 
Vậy số cần tìm là 456.

d)Khi viết thêm chữ số 6 vào bên phải số đó thì tức là số đó gấp lên 10 lần và 6 đơn vị hoặc tăng lên 9 lần bản thân nó và 6 đơn vị.
 9 lần số đó là:
3228 - 6 = 3222 
Số đó là 3222 :  9 = 358 
Vậy số cần tìm là 358.

Lời giải:
Gọi số cần tìm là $\overline{ab}$. Điều kiện: $a,b$ là số tự nhiên; $a,b\leq 9; a\neq 0$

Theo bài ra ta có:

$\overline{ab3}-\overline{ab}=471$

$\overline{ab}\times 10+3-\overline{ab}=471$

$\overline{ab}\times (10-1)+3=471$

$\overline{ab}\times 9+3=471$

$\overline{ab}\times 9=468$

$\overline{ab}=468:9=52$
Vậy số cần tìm là $52$

Giải:

Gọi số cần tìm là x, ta có:

x3 - x = 471

x. 10 + 3 - x = 471

10x - x + 3 = 471

9x + 3 =471

9x = 471 - 3

9x = 468

x = 468 : 9

x = 52

Vậy số cần tìm là 52.

*Dấu chấm trên bài là dấu nhân nha*

Gọi số đó là: \(\overline{ab}\)

Theo đề ta có: \(\overline{2ab2}\)

Mà: \(\overline{2ab2}=2000+\overline{ab}\times10+2\) lớn hơn số \(\overline{ab}\) 2443 đơn vị

\(\Rightarrow\left(2000+\overline{ab}\times10+2\right)-\overline{ab}=2443\)

\(2000+\overline{ab}\times10+2-\overline{ab}=2443\)

\(2002+\overline{ab}\times\left(10-1\right)=2443\)

\(2002+\overline{ab}\times9=2443\)

\(\overline{ab}\times9=2443-2002\)

\(\overline{ab}\times9=441\)

\(\overline{ab}=441:9=49\)

Vậy số cần tìm là 49

giúp bạn ấy đi

ai biết mà giúp

Gọi số cần tìm là ab ( có gạch ngang trên đầu)
Theo bài ra ta có:  a - b =5 (1)
nếu viết xen chữ số 0 vào giữa số hàng chục và hàng đơn vị thì số mới là: a0b ( có gạch ngang trên đầu)
=> a0b - ab = 630
=> 100a + 0 + b - 10a - b = 630
=> 90a = 630
=> a = 7
Thay a = 7 vào (1) ta đc b=2
Vậy số cần tìm là 72

học tốt

Gọi số cần tìm là ab, ta có:

ab + 630 = a0b

a x 10 + b + 630 = a x 100 + b

b + 630 - b = a x 100 - a x 10

630 = a x 90 \(\Rightarrow a=7\)

\(\Rightarrow b=7-5=2\)

Vậy số cần tìm là 72.

Gọi \(a\)là chữ số hàng chục, \(b\)là chữ số hàng đơn vị.

Điều kiện \(0< a\le9;0\le b\le9\)và \(a,b\inℕ\)

Khi đó số tự nhiên cần tìm là \(\overline{ab}\)

Vì chữ số hàng chục lớn hơn chữ số hàng đơn vị là \(5\)nên ta có phương trình : \(a-b=5\)\(\left(1\right)\)

Viết chữ số \(0\)vào giữa số hàng chục và chữ số hàng đơn vị, ta được chữ số mới là \(\overline{a0b}\)

Vì số mới lớn hơn số cũ \(630\)đơn vị nên ta có phương trình : \(\overline{a0b}-\overline{ab}=630\)\(\left(2\right)\)

Từ \(\left(1\right)\)và \(\left(2\right)\)ta có hệ phương trình \(\hept{\begin{cases}a-b=5\\\overline{a0b}-\overline{ab}=630\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}a-b=5\\\left(100a+b\right)-\left(10a+b\right)=630\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}a-b=5\\90a=630\end{cases}\Leftrightarrow\hept{\begin{cases}a-b=5\\a=7\end{cases}}}\)\(\Leftrightarrow\hept{\begin{cases}b=2\\a=7\end{cases}}\)(thỏa mãn)

Vậy số cần tìm là \(72\)

khi viết thêm chữ số 8 vào bên phải số đó thì số đó gấp lên 10 và 8 đơn vị

 hiệu số phần băng nhau là

10 - 1 = 9  phần

số đó là

( 485 - 8 ) : 9 = 53

         đáp số : 53