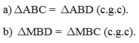Cho tam giác ABC vuông ở . Trên tia đối của tia AC lấy K sao cho AK = AC .
a) Chứng minh tam giác ABC = tam giác ABK .
b) Trên tia đối của tia AB lấy M . Chứng minh tam giác MBK = tam giác MBC .

Những câu hỏi liên quan
cho tam giác ABC vuông tại A. trên tia đối của tia AC lấy điểm D sao cho AD = AC.
a) chứng minh tam giác ABC = tam giác ABD
b) trên tia đối cua tia AB lấy điểm M. chứng minh tam giác MBD = tam giác MBC
Bài 5: Cho tam giác ABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho
AD = AC.
a. Chứng minh tam giác AABC = tam giác ABD
b. Trên tia đối của tia AB, lấy điểm M. Chứng minh tam giác MBD= tam giác MBC. ai vẽ hình cho mình với nha !!!!
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
AB chung
AC=AD
Do đó: ΔABC=ΔABD
Suy ra: ABC=ABD
Đúng 0
Bình luận (1)
b) Vì △ABC = △ABD
=> BC = BD và ˆABC=ˆABDABC^=ABD^
Xét tam giác △MBD và △MBC
Có MB: cạnh chung
MBD=MBC
BD = BC
=> △MBD = △MBC
Đúng 0
Bình luận (2)
cho tam giác abc có ab=ac,vẽ tia ak là phân giác của góc bac(k thuộc bc);a)chứng minh tam giác abk=tam giác ack;b)chứng minh ak vuông góc với bc;c)trên tia đối của tia ka lấy điểm h sao cho kh=ka chứng minh ab=ch
a: Xét ΔABK và ΔACK có
AB=AC
\(\widehat{BAK}=\widehat{CAK}\)
AK chung
Do đó: ΔABK=ΔACK
b: Ta có: ΔABC cân tại A
mà AK là đường phân giác
nên AK là đường cao
c: Xét tứ giác ABHC có
K là trung điểm của BC
K là trung điểm của AH
Do đó: ABHC là hình bình hành
Suy ra: AB=CH
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A, có AB=AC=13cm, BC=24cm. Kẻ AH vuông góc với BC tại H
a) Chứng minh tam giác AHC = tam giác AHB
b)Tính độ dài đoạn thẳng AH
c)Trên tia đối của tia BC lấy điểm K, trên tia đối của tia CB lấy, điểm I sao cho BK=CI. CMR tam giác ABK = tam giác ACI
d) kẻ BM vuông AK, CN vuông AI .CMR tam giác MBK = tam giác NCI
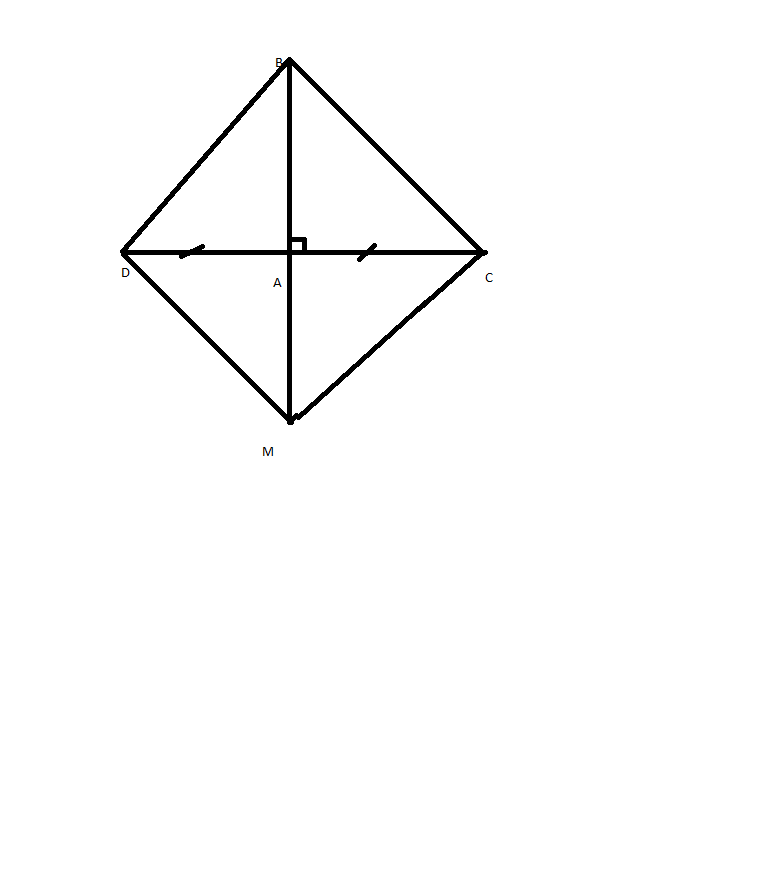
GT | △ABC cân tại A. AB = AC = 13cm. BC = 24cm. AH ⊥ BC (H |
KL | a, △AHC = △AHB b, AH = ? c, △ABK = △ACI d, △MBK = △NCI |
Bài giải:
a, Vì △ABC cân tại A (gt) => AB = AC và ABC = ACB
Xét △AHC vuông tại H và △AHB vuông tại H
Có: AH là cạnh hcung
AC = AB (cmt)
=> △AHC = △AHB (ch-cgv)
b, Ta có: BC = BH + HC
Mà BC = 24 cm
=> BH + HC = 24 cm
Mà HC = HB (△AHC = △AHB)
=> HC = HB = 24 : 2 = 12 (cm)
Xét △ABH vuông tại H có: AH2 + BH2 = AB2 (định lý Pytago)
=> AH2 + 122 = 132 => AH2 = 25 => AH = 5
c, Ta có: ABK + ABC = 180o (2 góc kề bù)
ACI + ACB = 180o (2 góc kề bù)
Mà ABC = ACB (cmt)
=> ABK = ACI
Xét △ABK và △ACI
Có: AB = AC (cmt)
ABK = ACI (cmt)
BK = CI (gt)
=> △ABK = △ACI (c.g.c)
d, Xét △MBK vuông tại M và △NCI vuông tại N
Có: BK = CI (gt)
MKB = NIC (△ABK = △ACI)
=> △MBK = △NCI (ch-gn)
cho tam giác abc vuông ở a.trên tia dối của ac lấy điểm d sao cho ad=ac.
a;chứng minh tam giác abc=tam giác abd
b;trên tia đối của tia ab lấy điểm m.chứng minh tam giác mbd=tam giác mbc
a)Vì góc BAC và góc DAB là 2 góc kề bù
Mà BAC=90°->DAB=180°-BAC=90°
Xét ∆ABC và ∆ABD
-AB chung
-AC=AD(gt)
-BAC =DAC(cmt)
->∆ABC=∆ABD(c.g.c)
b)Xét ∆MBD và ∆MBC
-BC=BD(Do ∆ABC=∆ABD cmt)
-AC =AD(gt)
->∆MBD=∆MBC(cạnh huyền cạnh góc vuông)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
a) Chứng minh ∆ A B C = ∆ A B D .
b) Trên tia đối của tia AB lấy điểm M. Chứng minh ∆ M B D = ∆ M B C .
Cho tam giác ABC có AB < AC. Trên cạnh AC lấy điểm D sao cho AD = AB. Gọi M là trung điểm cạnh BD.
a) Chứng minh: Tam giác ABM = Tam giác ADM
b) Tia AM cắt BC tại K. Chứng minh: AK vuông góc với BD
c) Trên tia đối của tia đối của tia BA lấy điểm E sao cho BE=DC.Chứng minh D,K,E thẳng hàng
giải giúp mình nha cảm ơn các bạn nhiều
Cho tam giác ABC có AB < AC. Trên cạnh AC lấy điểm D sao cho AD = AB. Gọi M là trung điểm cạnh BD.
a) Chứng minh: Tam giác ABM = Tam giác ADM
b) Tia AM cắt BC tại K. Chứng minh: AK vuông góc với BD
c) Trên tia đối của tia đối của tia BA lấy điểm E sao cho BE=DC.Chứng minh D,K,E thẳng hàng
a: Xét ΔABM và ΔADM có
AB=AD
AM chung
BM=DM
Do đó: ΔABM=ΔADM
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A . trên tia đối của tia AC lấy điểm D sao cho AD=AC
a) chúng minh tam giác ABC = tam giác ABD
b) trên tia đối của tia AB , lấy điểm M . chúng minh tam giác MBD = tam giác MBC
Tự vẽ hình nhé ?
a) Vì tam giác ABC vuông tại A (GT)
=> Góc BAC = 90o (ĐN)
Mà góc BAC + góc BAD = 180o (kề bù)
=> Góc BAC = góc BAD = 180o : 2 = 90o (1)
Xét tam giác ABC và tam giác ABD có :
AC = AD (GT)
Góc BAC = góc BAD = 90o (Theo (1))
AB chung
=> Tam giác ABC = tam giác ABD (c.g.c) (2)
b) Từ (2) => Góc ABC = góc ABD (2 góc tương ứng)
Mà góc ABC + góc MBC = 180o (kề bù)
góc ABD + góc MBD = 180o (kề bù)
=> Góc MBC = góc MBD (3)
Từ (2) => BC = BD (2 cạnh tương ứng) (4)
Xét tam giác MBD và tam giác MBC có :
BM chung
Góc MBD = góc MBC (Theo (3))
BD = BD (Theo (4))
=> Tam giác MBD = tam giác MBC (c.g.c)
Vậy ...
a) Xét tam giác ABC và tam giác ABD có :
AD=AC (GT)
góc BAD = góc BAC (=90 độ)
AB là cạnh chung
=> tam giác ABC = tam giác ABD (c-g-c)
b) vì tam giác ABC = tam giác ABD (cmt)
=> BD=BC ( 2 cạnh tương ứng)
góc B1 = góc B2 (2 góc tương ứng)
Xét tam giác MBD và tam giác MBC có :
BD=BC (cmt)
góc B1 = góc B2 (cmt)
BM là cạnh chung
=>tam giác MBD=tam giác MBC (c-g-c)
a ) Xét △ABC vuông tại A và △ABD vuông tại A có :
AC = AD ( gt )
góc BAD = góc BAC = 90 độ
BA là cạnh chung
=> △ABC = △ABD ( c.g.c )
b ) Vì △ABC = △ABD ( cmt )
=> BD = BC ( 2 cạnh tương ứng )
Ta có : CBA + CBM = 180o ( 2 góc kề bù )
DBA + DBM = 180o ( 2 góc kề bù )
Mà : ABC = ABD ( cmt )
=> CBM = DBM
Xét △CBM và △DBM có :
BC = BD ( cmt )
CBM = DBM ( cmt )
BM là cạnh chung
=> △CBM = △DBM ( c.g.c )
Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC
a, Chứng minh: tam giác ABC= tam giác ABD
b, Trên tia đối của tia AB lấy điểm M. Chứng minh: tam giác MBD=tam giác MCB
Tam giác ABC vuông tại A => tam giác ABD cũng vuông tại D
a) Xét 2 tam giác : ABD và BẮC, ta có:
AD = AC (GT)
AB LÀ CẠNH CHUNG
vậy tam giác ABD = tam giác ABC ( 2 cạnh góc vuông bằng nhau )
b) Từ tam giác ABD = tam giác ABC ( 2 cạnh góc vuông bằng nhau )
=> góc ABD = góc ABC ( 2 góc tương ứng )
=> BD = BC ( 2 CẠNH TƯƠNG ỨNG )
Xét 2 tam giác : MBD và MCB, ta có :
BM là cạnh chung
góc ABD = góc ABC
BD = BC
=> tam giác MBD = TAM GIÁC MCB ( c . g. c)
ko sai đâu
Đúng 1
Bình luận (0)
Tam giác ABC vuông tại A => tam giác ABD cũng vuông tại D
a) Xét 2 tam giác : ABD và BẮC, ta có:
AD = AC (GT)
AB LÀ CẠNH CHUNG
vậy tam giác ABD = tam giác ABC ( 2 cạnh góc vuông bằng nhau )
b) Từ tam giác ABD = tam giác ABC ( 2 cạnh góc vuông bằng nhau )
=> góc ABD = góc ABC ( 2 góc tương ứng )
=> BD = BC ( 2 CẠNH TƯƠNG ỨNG )
Xét 2 tam giác : MBD và MCB, ta có :
BM là cạnh chung
góc ABD = góc ABC
BD = BC
=> tam giác MBD = TAM GIÁC MCB ( c . g. c)
chính xác, nhớ like nhoa!!!!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời









 BC). BK = CI. BM ⊥ AK. CN ⊥ AI
BC). BK = CI. BM ⊥ AK. CN ⊥ AI