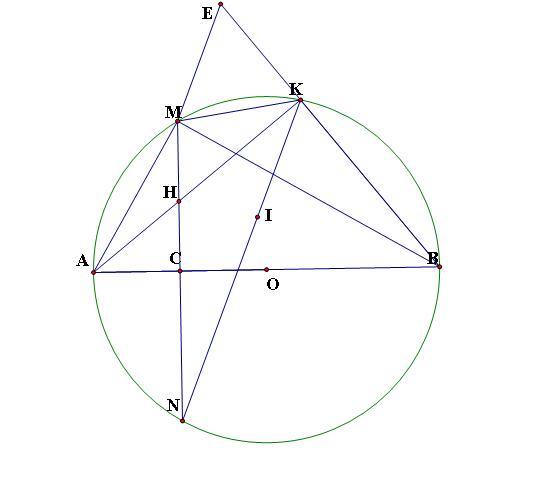
Cho đuong tron tâm O đường kính AB= 2R . gọi C là trung điểm OA qua C kẻ dây MN vuông goc với AO tại C . Gọi K là điểm tuỳ ý trên cung nhỏ BM , H là giao điểm của AK và MN .
a) Chứng minh BCHK là tu giac nội tiep b) Chứng minh AK.AH = R2 c) Trên KN lây điểm I sao cho KI = KM , chứng minh NI= KB Mọi người giúp em với ạ em không biết làm câu c) thôi