Phát biểu a) là phát biểu sai. Vì một tam giác đều khi có ba cạnh bằng nhau không nhất thiết phải bằng 2cm, có thể bằng 3cm, 4cm, …

Phát biểu b) là đúng. Vì tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau.

Phát biểu c) là sai. Vì tam giác IKH chỉ có hai cạnh và hai góc bằng nhau nên chưa đủ điều kiện để tam giác IKH là tam giác đều.

k đúng mình mình giải cho

a,b,c sai còn d đúng

Giải thích vẽ hình ra sẽ thấy

Có bn nào bt trình bày k

a: \(\widehat{P}=180^0-80^0-60^0=40^0< \widehat{N}< \widehat{M}\)

nên MN<MP<NP

c: Đúng

d: Sai vì chỉ có tâm đường tròn ngoại tiếp cách đều 3 đỉnh thôi

ggggggggggggggggg

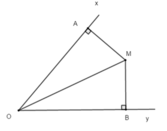
Gọi MA và MB theo thứ tự là khoảng cách từ M đến Ox và Oy

Xét hai tam giác vuông OMA và OMB có:

OM là cạnh chung

MA = MB (gt)

Do đó ΔOMA=ΔOMB (cạnh huyền – cạnh góc vuông)

Suy ra: M O A ^ = M O B ^ (hai góc tương ứng)

Vậy OM là tia phân giác của  x O y ^

Vậy thứ tự sắp xếp phải là: b, c, a, d, e.

Chọn đáp án A

ai giúp tớ tớ cho 5 ****

nha

Do tam giác ABC và A'B'C' có AB=A'B' ,AC=A'C'

Theo tính chất cạnh và góc đối diện,ta có:

Góc A >góc A' <=> BC>B'C' (đpcm)

b) tương tự như câu a ta có

BC>B'C' <=> Góc A >A'

CM: Ta có: \(\widehat{BIM}+\widehat{MIN}+\widehat{NIC}=\widehat{BIC}\)

=> \(\widehat{BIC}=2.30^0+90^0=150^0\)

Ta lại có : \(\widehat{FIB}+\widehat{BIC}=180^0\) (kề bù)

=> \(\widehat{FIB}=180^0-\widehat{BIC}=180^0-150^0=30^0\)

=> \(\widehat{FIB}=\widehat{EIC}=30^0\) (đối đỉnh)

Xét t/giác FIB và t/giác MIB

có : \(\widehat{B_1}=\widehat{B_2}\) (gt)

   BI : chung

  \(\widehat{FIB}=\widehat{BIM}=30^0\)  

=> t/giác FIB = t/giác  MIB (g.c.g)

=> BF = BM (2 cạnh t/ứng)

Xét t/giác EIC và t/giác NIC

có : \(\widehat{C_1}=\widehat{C_2}\) (gt) 

  IC : chung

   \(\widehat{EIC}=\widehat{NIC}=30^0\)

=> t/giác EIC = t/giác NIC (g.c.g)

=> EC = IN (2 cạnh t/ứng)

Ta có: BC = BM + MN + NC 

hay BC = BF + MN + EC

=> CE + BF = BC - MN  => CE + BF < BC (Đpcm)