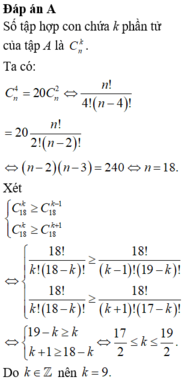Tìm số phần tử của tập hợp: A={2;4;6;…;104}

Những câu hỏi liên quan
Tập hợp A gồm n phần tử
n
≥
4
. Biết rằng số tập hợp con chứa 4 phần tử của A bằng 20 lần số tập hợp con chứa 2 phần tử của A. Tìm số
k
∈
1
;
2
;
.
.
.
;
n
sao cho số tập hợp con chứa k phần tử của A là lớn nhất. A. 9...
Đọc tiếp
Tập hợp A gồm n phần tử n ≥ 4 . Biết rằng số tập hợp con chứa 4 phần tử của A bằng 20 lần số tập hợp con chứa 2 phần tử của A. Tìm số k ∈ 1 ; 2 ; . . . ; n sao cho số tập hợp con chứa k phần tử của A là lớn nhất.
A. 9
B. 8
C. 7
D. 6
Cho A = { 1 ; 2 ; 3 } ; B = { 5 }
a tìm số phần tử của mỗi tập hợp
b viết các tập hợp con khác tập hợp rỗng của tập hợp A
c Viết tập hợp gồm 3 phần tử trong đó có 2 phần tử thuộc A và 1 phần tử thuộc B
câu a có 8 tập hợp con, câu b có 2tập hợp con
câu b)A có các tập hợp con là: 1; 2; 3;1và3;1và2;2và3;1,2và3.
B có các tập hợp con là: 5.
câu c)1,2và5;1,3và5; 2,3và5.
Đúng 0
Bình luận (0)
Cho hai tập hợp Hữu hạn A, B. Biết rằng số phần tử chung của A và B bằng nửa số phần tử của B và hợp của hai tập hợp A và B có 9 phần tử. Hãy tìm số phần tử của mỗi tập hợp đó
Cho hai tập hợp Hữu hạn A, B. Biết rằng số phần tử chung của A và B bằng nửa số phần tử của B và hợp của hai tập hợp A và B có 9 phần tử. Hãy tìm số phần tử của mỗi tập hợp đó
cho hai tập hợp A, B. Biết số phần tử chung của hai tập hợp bằng một nửa số phần tử của B và hợp của A và B có 7 phần tử. hãy tìm số phần tử của mỗi tập hợp
Có: nA + nB = n(A hợp B) + n(A giao B)
=> nA + nB = 7 + nB/2
=> 2nA + nB = 14
Vì n(A giao B) = nB/2 nên nA > nB/2 => 2nA > nB => 14 > 2nB => nB < 7
Mà nB/2 là số tự nhiên nên nB là số chẵn
\(\Rightarrow\left(nA,nB\right)=\left(7;0\right),\left(6;2\right),\left(5;4\right),\left(4;6\right)\)
Lúc này n(A giao B) lần lượt là 0; 1; 2; 3 ---> thỏa đề
Biết tập hợp a có số tập hợp con là 20302 có số phần của mỗi tập hợp đó ko vượt quá 2 . Tìm số phần tử của tập hợp
Cho tập hợp A gồm n phần tử (
n
≥
4
) , biết rằng số tập con gồm 4 phần tử của A bằng 20 lần số tập con gồm 2 phần tử của A. Tìm k (
1
≤
k
≤
n
) sao cho số tập con gồm k phần tử của A lớn nhất A. k 9 B. k 7 C. k 8 D. k 6
Đọc tiếp
Cho tập hợp A gồm n phần tử ( n ≥ 4 ) , biết rằng số tập con gồm 4 phần tử của A bằng 20 lần số tập con gồm 2 phần tử của A. Tìm k ( 1 ≤ k ≤ n ) sao cho số tập con gồm k phần tử của A lớn nhất
A. k = 9
B. k = 7
C. k = 8
D. k = 6
Câu 1: CMR: hai tâp hợp (A \ B) \ C = (A \ C) \ (B \ C)
Câu 2: Cho hai tâp hợp A và B. Biết số phần tử của tâp hợp A giao tập hợp B Bằng nửa số phần tử của B và số p hần tử tập hợp A hợp tập hợp B là 7. Hãy tìm số phần tử của các tập hơp đó
Cho tập hợp A gồm n phần tử \(\left(n\ge4\right)\). Biết rằng số tập hợp con gồm 4 phần tử của A bằng 20 lần số tập hợp con gồm 2 phần tử của A. Tìm \(k\in\left[1,2,.....,n\right]\) sao cho số tập con gồm k phần tử của tập hợp A là lớn nhất.
Số tập hợp con có k phần tử của tập hợp A (có 18 phần tử)
\(C_{18}^k\left(k=1,.....,18\right)\)
Để tìm max \(C_{18}^k,k\in\left\{1,2,.....,18\right\}\) (*), ta tiến hành giải bất phương trình sau :
\(\frac{C_{18}^k}{C_{18}^{k+1}}< 1\)
\(\Leftrightarrow C_{18}^k< C_{18}^{k+1}\)
\(\Leftrightarrow\frac{18!}{\left(18-k\right)!k!}< \frac{18!}{\left(17-k\right)!\left(k+1\right)!}\)
\(\Leftrightarrow\left(18-k\right)!k!>\left(17-k\right)!\left(k+1\right)!\)
\(\Leftrightarrow17>2k\)
\(\Leftrightarrow k< \frac{17}{2}\)
Điều kiện (*) nên k = 1,2,3,.....8
Suy ra \(\frac{C_{18}^k}{C_{18}^{k+1}}>1\) khi k = 9,10,...,17
Vậy ta có
\(C^1_{18}< C_{18}^2< C_{18}^3< .........C_{18}^8< C_{18}^9>C_{18}^{10}>.....>C_{18}^{18}\)
Vậy \(C_{18}^k\) đạt giá trị lớn nhất khi k = 9. Như thế số tập hợp con gồm 9 phần tử của A là số tập hợp con lớn nhất.
Đúng 0
Bình luận (0)
1 >tìm số phần của tập hợp B gồm các số tuej nhiên lẻ có 3 chứ số
2) cho A =(0,2,4 :...100) và B là tập hợp các số chia hết cho 5 và nhỏ hơn 100.Gọi C là tập hợp gồm các phần tử thuộc tâp B và không thuộc tập hợp a .tìm số phần tử của tập C