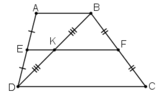
+ ΔABD có DE = EA và DK = KB

⇒ EK là đường trung bình của ΔDAB

⇒ EK // AB

+ Hình thang ABCD có: AE = ED và BF = FC

⇒ EF là đường trung bình của hình thang ABCD

⇒ EF // AB// CD

+ Qua điểm E ta có EK // AB và EF // AB nên theo tiên đề Ơclit ta có E, K, F thẳng hàng.

Xét ΔDAB có

E là trung điểm của AD

K là trung điểm của BD

Do đó: EK//AB

hay EK//CD

Xét ΔBDC có 

K là trung điểm của BD

F là trung điểm của BC

Do đó: KF là đường trung bình của ΔBDC

Suy ra: KF//DC

Ta có: EK//DC

KF//DC

mà KE và KF có điểm chung là K

nên E,K,F thẳng hàng

Ta có E và F là trung điểm của AD và BC

=> EF là ĐTB của hình thang ABCD

=> EF//AB//CD

Do F,K là trung điểm cuả BD và BC

=> FK là ĐTB của tam giác ADC

=> FK//CD

Do E và K là trung điểm của AD và BD

=> EK là ĐTB của tam giác ABD

=> EK//AB

Mà AB//CD

=>EF ; EK ; FK cùng // với AB 

=> E ; F ; K thẳng hàng

Bài giải:

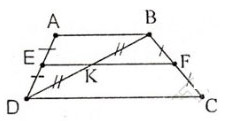
Ta có EA = ED, KB = KD (gt)

Nên EK // AB

Lại có FB = FC, KB = KD (gt)

Nên KF // DC // AB

Qua K ta có KE và KF cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.

\(\Delta ADB\) có:\(AE=DE\left(gt\right),BF=FD\left(gt\right)\)

\(\Rightarrow AB\) // \(EF\)(theo đlí 2 về đường trung bình của tam giác) (1)

\(\Delta BDC\) có:\(BK=KC\left(gt\right),BF=FD\left(gt\right)\)

\(\Rightarrow FK\) // \(CD\)(theo đlí 2 về đường trung bình của tam giác)

Mà \(CD\) // \(AB\Rightarrow FK\) // \(AB\) (1)

Từ (1) và (2), suy ra:

\(AB\) // \(EF,FK\)

\(\Rightarrow E,F,K\) thẳng hàng (theo tiên đề Ơclit )

tham khảo bài mk nha!

Vì E là trung điểm của AD và BC => EF là đường trung bình của hình thang ABCD => EF//AB//CD

Do E và K là trung điểm của AD và BD => EK là đường trung bình của tam giác ABD => EK//AB

Do F và K là trung điểm của BC và BD => FK là đường trung bình của tam giác BCD => FK//BC

Mà AB//CD => EF;EK;FK cùng song song với AB => E,F,K thẳng hàng.

đề bài kiểu gì vậy bạn??

có gì sai hả bạn?

phần các độn cắt nhau á bạn, mình thấy vô lý quá, không ra cái hình gì cả