A và B chuyển động với vận tốc đều trên 2 đường thẳng vuông góc với nhau tại O. Khi A đến O thì B còn cách O là 500 mét. Hai phút sau họ cách đều O và 8 phút sau họ lại cách đều O. Hỏi tỉ số vận tốc của A đối với B?

Những câu hỏi liên quan
A và B chuyển động với vận tốc đều trên 2 đường thẳng vuông góc với nhau tại O. Khi A đến O thì B còn cách O là 500 mét. Hai phút sau họ cách đều O và 8 phút sau họ lại cách đều O. Hỏi tỉ số vận tốc của A đối với B?
Theo giả thiết: sau 2 phút thì A,B cách đều O, sau đó 8 phút lại tiếp tục cách đều. Suy ra quãng đường đi trong 8 phút sau của B bằng quãng đường mà A đi trong 10 phút. Vậy tỉ số vận tốc của A đối với B bằng \(\frac{8}{10}=\frac{4}{5}.\)
Đúng 0
Bình luận (0)
A và B chuyển động với vận tốc đều trên 2 đường thẳng vuông góc với nhau tại O. Khi A đến O thì B còn cách O là 500 mét. Hai phút sau họ cách đều O và 8 phút sau họ lại cách đều O. Hỏi tỉ số vận tốc của A đối với B?
Hai xe A và B chuyển động thẳng đều với cùng vận tốc V hướng đến o theo các quĩ đạo là những đường thẳng hợp với nhau góc α 60°. Biết ban đầu xe A và xe B cách O những khoảng AO 20 km và BO 30 km. Khoảng cách nhỏ nhất giữa hai xe gần với giá trị nào nhất sau đây?
A. 20 m/s B. 9 m/s C. 15m/s D. 6 m/s
Đọc tiếp
Hai xe A và B chuyển động thẳng đều với cùng vận tốc V hướng đến o theo các quĩ đạo là những đường thẳng hợp với nhau góc α = 60°. Biết ban đầu xe A và xe B cách O những khoảng AO = 20 km và BO = 30 km. Khoảng cách nhỏ nhất giữa hai xe gần với giá trị nào nhất sau đây?
A. 20 m/s
B. 9 m/s
C. 15m/s
D. 6 m/s
Chọn B
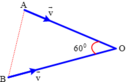
− Phương trình chuyển động xe A và xe B:
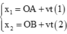
− Khoảng cách hai xe vào thời điểm t:
![]()
![]()
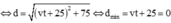
![]()
Đúng 0
Bình luận (0)
Hai xe A và B chuyển động thẳng đều với cùng vận tốc V hướng đến o theo các quĩ đạo là những đường thẳng hợp với nhau góc α 60°. Biết ban đầu xe A và xe B cách O những khoảng AO 20 km và BO 30 km. Khoảng cách nhỏ nhất giữa hai xe gần với giá trị nào nhất sau đây?
A. 20 m/s B. 9 m/s C. 15m/s D. 6 m/s
Đọc tiếp
Hai xe A và B chuyển động thẳng đều với cùng vận tốc V hướng đến o theo các quĩ đạo là những đường thẳng hợp với nhau góc α = 60°. Biết ban đầu xe A và xe B cách O những khoảng AO = 20 km và BO = 30 km. Khoảng cách nhỏ nhất giữa hai xe gần với giá trị nào nhất sau đây?
A. 20 m/s
B. 9 m/s
C. 15m/s
D. 6 m/s
Chọn B
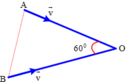
− Phương trình chuyển động xe A và xe B:
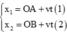
− Khoảng cách hai xe vào thời điểm t:
![]()
![]()
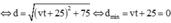
![]()
Đúng 0
Bình luận (0)
Hai địa điểm A và B cách nhau 700m. Xe 1 khởi hành từ A chuyển động thẳng đều đến B với vận tốc v1. Xe 2 khởi hành từ B cùng lúc với xe 1, chuyển động thẳng đều với vận tốc v2. Cho biết: -Khi xe 2 chuyển động trên đường AB về phía A, hai xe gặp nhau khi chuyển động đc 50s. -Khi xe 2 chuyển động trên đường AB ra xa A, hai xe gặp nhau khi chuyển động đc 350s. 1/ Tìm v1, v2 2/ Nếu xe 2 chuyển động trên đường vuông góc với AB thì bao lâu sau khi chuyển động, khoảng cách giữa hai xe là ngắn nhất. Kho...
Đọc tiếp
Hai địa điểm A và B cách nhau 700m. Xe 1 khởi hành từ A chuyển động thẳng đều đến B với vận tốc v1. Xe 2 khởi hành từ B cùng lúc với xe 1, chuyển động thẳng đều với vận tốc v2. Cho biết: -Khi xe 2 chuyển động trên đường AB về phía A, hai xe gặp nhau khi chuyển động đc 50s. -Khi xe 2 chuyển động trên đường AB ra xa A, hai xe gặp nhau khi chuyển động đc 350s. 1/ Tìm v1, v2 2/ Nếu xe 2 chuyển động trên đường vuông góc với AB thì bao lâu sau khi chuyển động, khoảng cách giữa hai xe là ngắn nhất. Khoảng cách này là bao nhiêu?
a). Khi xe II đi về phía A:
V1+V2=![]() =
= ![]()
![]()
Khi xe II đi ra xa A:
V1-V2=![]()
Lấy (1)+(2), ta được 2V1=16
![]()
![]() b. Gọi t là thời gian chuyển động của hai xe
b. Gọi t là thời gian chuyển động của hai xe

![]() B1
B1
A A1 B
Xe I đi đoạn AA1:
AA1=V1.t=8t
![]() Suy ra: A1B=700-8t
Suy ra: A1B=700-8t
Xe II đi đoạn BB1:
BB1=V2.t=6t
Xét tam giác A1BB1 vuông tại B có:
![]()
![]()


A1B1 nhỏ nhất khi:
10t-560=0
t=56 giây
minA1B1=![]() =420m
=420m
Đúng 0
Bình luận (0)
Một oto chuyển động thẳng đều từ A đến B với vận tốc 90km/h. Sau 15phút từ B một xe máy chuyển động về A với vận tốc 40km/h. Sau khi đến B oto dừng lại nghỉ 30 phút rồi chuyển động thẳng đều quay trở lại A và gặp xe máy lần 2 ở điểm cách A là 25km (chưa đến A) . Độ dài quãng đường AB là:
A. 115km
B. 215km
C. 90km
D. 25km
một ôtô chuyển động từ A đến B với vận tốc 54 km/ giờ trong 30 phút và trên đoạn đường còn lại là 72km với vận tốc 48 km/ giờ.A) Đoạn đường nào oto chuyển động nhanh hơn? B)Tính vận tốc trung bình của oto khi đi từ A đến BC) Đi từ A đến B theo chiều ban đầu ôt tiếp tục chuyển động đều đến vị trí C cách A 136 km/ giờ với vận tốc 50km/ giờ. lúc đó tại C có 1 xe máy chuyển động đều với vận tốc 40 km/ giờ theo chiều ban đầu chuyển động, sau bao lâu thì gặp xe ôto
Đọc tiếp
một ôtô chuyển động từ A đến B với vận tốc 54 km/ giờ trong 30 phút và trên đoạn đường còn lại là 72km với vận tốc 48 km/ giờ.
A) Đoạn đường nào oto chuyển động nhanh hơn?
B)Tính vận tốc trung bình của oto khi đi từ A đến B
C) Đi từ A đến B theo chiều ban đầu ôt tiếp tục chuyển động đều đến vị trí C cách A 136 km/ giờ với vận tốc 50km/ giờ. lúc đó tại C có 1 xe máy chuyển động đều với vận tốc 40 km/ giờ theo chiều ban đầu chuyển động, sau bao lâu thì gặp xe ôto
Hai xe máy đồng thời xuất phát, chuyển động đều đi lại gặp nhau, xe 1 đi từ thành phố A đến thành phố B và xe 2 đi từ thành phố B đến thành phố A. Sau khi gặp nhau tại C cách A 30km, hai xe tiếp tục hành trình của mình với vận tốc cũ. Khi đã tới nơi quy định (xe 1 tới B, xe 2 tới A), cả hai xe đều quay ngay trở về và gặp nhau lần thứ hai tại D cách B một đoạn 36 km. Coi quãng đường AB là thẳng, vận tốc của hai xe không thay đổi trong quá trình chuyển động. Tìm khoảng cách AB và tỉ số vận tốc của...
Đọc tiếp
Hai xe máy đồng thời xuất phát, chuyển động đều đi lại gặp nhau, xe 1 đi từ thành phố A đến thành phố B và xe 2 đi từ thành phố B đến thành phố A. Sau khi gặp nhau tại C cách A 30km, hai xe tiếp tục hành trình của mình với vận tốc cũ. Khi đã tới nơi quy định (xe 1 tới B, xe 2 tới A), cả hai xe đều quay ngay trở về và gặp nhau lần thứ hai tại D cách B một đoạn 36 km. Coi quãng đường AB là thẳng, vận tốc của hai xe không thay đổi trong quá trình chuyển động. Tìm khoảng cách AB và tỉ số vận tốc của hai xe.
Gọi \(v_1\) là vận tốc của xe xuất phát từ A, \(v_2\) là vận tốc của xe xuất phát từ B, \(t_1\) là khoảng thời gian từ lúc xuất phát đến lúc gặp nhau lần 1, \(t_2\) là khoảng thời gian từ lúc gặp nhau lần 1đến lúc gặp nhau lần 2 và đặt x = AB.
Gặp nhau lần 1: \(v_1t_1=30,v_2t_1=x-30\) suy ra \(\frac{v_1}{v_2}=\frac{30}{x-30}\)
Gặp nhau lần 2: \(v_1t_2=\left(x-30\right)+36=x+6;\)\(v_2t_2=30+\left(x-36\right)=x-6\)
suy ra \(\frac{v_1}{v_2}=\frac{x+6}{x-6}\)
Từ (1) và (2) suy ra x = 54km.
Thay x = 54 km vào (1) ta được \(\frac{v_1}{v_2}=1,25\) hay \(\frac{v_2}{v_1}=0,8\)
Đúng 3
Bình luận (4)
Hai xe A và B chuyển động trên hai đường thẳng vuông góc với nhau. Xe A đi vớivận tốc là v1 3 m/s. Xe B đi với vận tốc v2 4 m/s. Vào thời điểm xe A đi qua giaođiểm O của hai đường thẳng thì xe B cách O là 80 m và đang tiến lại gần O.a) Vẽ hình mô tả chuyển động của 2 xe vào thời điểm xe A đi qua giao điểm O.b) Sau thời điểm nói trên t 10 s thì hai xe cách nhau bao nhiêu?c) Tìm khoảng cách nhỏ nhất giữa hai xe trong khi chuyển động?giúp tớ với
Đọc tiếp
Hai xe A và B chuyển động trên hai đường thẳng vuông góc với nhau. Xe A đi với
vận tốc là v1 = 3 m/s. Xe B đi với vận tốc v2 = 4 m/s. Vào thời điểm xe A đi qua giao
điểm O của hai đường thẳng thì xe B cách O là 80 m và đang tiến lại gần O.
a) Vẽ hình mô tả chuyển động của 2 xe vào thời điểm xe A đi qua giao điểm O.
b) Sau thời điểm nói trên t = 10 s thì hai xe cách nhau bao nhiêu?
c) Tìm khoảng cách nhỏ nhất giữa hai xe trong khi chuyển động?
giúp tớ với













