de bai truc trac con cac

Tại các bạn không hiểu đề bài thôi

Em vừa nghĩ ra 2 cách làm bằng kiến thức lớp 7, co check giùm em nhé!

Ta có: \(\widehat{CAD}=90^0-\widehat{DAB}\)

và \(\widehat{CDA}=90^0-\widehat{HAD}\)

Mà \(\widehat{DAB}=\widehat{HAD}\left(gt\right)\Rightarrow AC=DC\)

Tương tự ta có: AB = EB

\(\Rightarrow AB+AC=EB+DC\)

\(=ED+DB+DC=DE+BC\)

\(\Rightarrow DE=AB+AC-BC=3+4-5=2\left(cm\right)\)

Vậy DE = 2 cm

Ta có: \(\Delta\)ABC vuông tại A

=> BC\(^2\)=AB\(^2\)+ AC\(^2\)= 3\(^2\)+ 4\(^2\)=  25 => BC = 5 (cm)

Có: \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AB^2}=\frac{1}{3^2}+\frac{1}{4^2}=\frac{25}{144}\)

=> AH = 2,4  (cm)

Có: \(CH=\frac{AC^2}{BC}=\frac{4^2}{5}=3,2\)(cm)

=> BH = 5 - 3,2 = 1,8 ( cm )

AE là phân giác ^CAH => \(\frac{EC}{EH}=\frac{AC}{AH}=\frac{4}{2,4}\) mà EC + EH = CH = 3,2 

=> EC = 2 ( cm ) ; EH = 1,2 ( cm )

AD là phân giác ^BAH  => \(\frac{DH}{DB}=\frac{AH}{AB}=\frac{2,4}{3}\); mà DH + DB = HB = 1,8 

=> DH = 0,8 ( cm ) ; BD = 1( cm )

Vậy DE = DH + HE = 0,8 + 1,2 = 2 ( cm )

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có

BD chung

góc ABD=góc HBD

=>ΔBAD=ΔBHD

b: ΔBAD=ΔBHD

=>DA=DH

mà DH<DC

nên DA<DC

c: Xét ΔDAK vuông tại A và ΔDHC vuông tại H có

DA=DH

AK=HC

=>ΔDAK=ΔDHC

=>góc ADK=góc HDC

=>góc HDC+góc KDC=180 độ

=>K,D,H thẳng hàng

a: Xét ΔAMD vuông tại M và ΔAND vuông tại N có

AD chung

góc MAD=góc NAD

=>ΔMAD=ΔNAD

=>AM=AN

b: Xét ΔACB có AM/AB=AN/AC

nên MN//BC

c: Xét ΔADE có

AM vừa là đường cao, vừa là trung tuýen

=>ΔADE cân tại A

=>AD=AE

Xét ΔADF có

AN vừa là đường cao, vừa là trung tuyến

=>ΔADF cân tại A

=>AD=AF

=>AE=AF

=>ΔAEFcân tạiA

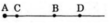
Điểm D thuộc tia đối của tia BC nên điểm B nằm giữa hai điểm C và D.

Do đó: CD = CB + BD = 3 + 2 = 5cm

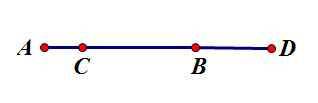
\(a.\) \(CB=AB-AC=4-1=3\) \(cm\)
\(b.\) \(CD=CB+BD=3+2=5\) \(cm\)

2:

a: OA và OB là hai tia đối nhau

=>O nằm giữa A và B

mà OA=OB

nên O là trung điểm của AB

b: OC<OB

=>C nằm giữa O và B

mà OC=1/2OB

nên C là trung điểm của OB