Chứng minh rằng : Nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại A
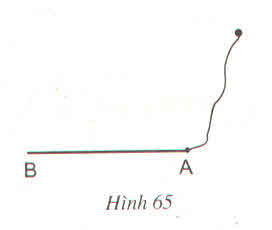
Ứng dụng : Một tờ giấy bị rách ở mép (h.65). Hãy dùng thước và compa dựng đường vuông góc với cạnh AB tại A
Chứng minh rằng: Nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại A.
Ứng dụng: Một tờ giấy bị rách mép (h.65). Hãy dùng thước và compa dựng đường vuông góc với cạnh AB tại A.
Chứng minh rằng "Nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại A"
Ta có : MA = MB = MC ( suy từ gt ) .
Các tam giác MAB, MAC cân tại M
Suy ra : \(\widehat{A_1}=\widehat{B}\); \(\widehat{A_2}=\widehat{C}\)( hai góc ở đáy )
Vậy \(\widehat{A_1}+\widehat{A_2}=\widehat{B}+\widehat{C}\)hay \(\widehat{A}=\widehat{B}+\widehat{C}=\frac{180^o}{2}=90^o\)
Vậy \(\Delta ABC\)vuông tại A
a,c/m rằng: trong 1 tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền.
b, c/m rằng: nếu tam giác abc có đường trung tuyến xuất phát từ a bằng 1 nửa cạnh bc thì đó là tam giác vuông tại a.
Ứng dụng: Một tờ giấy bị rách ở mép (h.110). Hãy dùng thước và compa vẽ đường vuông góc với AB tại A.
Hướng dẫn: Vẽ điểm C sao cho CA = CB, rồi vẽ điểm E thuộc tia đối của tia CB sao cho CE = CB.
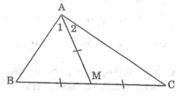
ΔABE có đường trung tuyến AC bằng 1/2 BE nên ∠(BAE) = 90o.
Vậy AE ⊥ AB.
Chứng minh rằng: Nếu tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC thì tam giác đo vuông tại A.
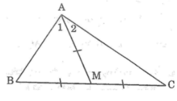
Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC
Mà AM = 1/2 BC (gt) nên: AM = BM = MC.
Tam giác AMB có AM = MB nên ΔAMB cân tại M
Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)
Tam giác AMC có AM = MC nên ΔAMC cân tại M
Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠(BAC) (3)
Trong ΔABC ta có:
∠B + ∠C + ∠(BAC) = 180o (tổng ba góc trong tam giác) (4)
Từ (3) và (4) suy ra: ∠(BAC) + ∠(BAC) = 180o ⇔ 2∠(BAC) = 180o
Hay ∠(BAC) = 90o.
Vậy ΔABC vuông tại A.
Chứng minh rằng: Nếu 1 tam giác có đường cao và đường trung tuyến ứng với 1 cạnh (xuất phát từ 1 đỉnh) chia góc ở đỉnh đó thành 3 phần bằng nhau thì tam giác ấy vuông
Chứng minh rằng nếu trong tam giác ABC có hai cạnh AB và AC không bằng nhau thì đường trung tuyến xuất phát từ đỉnh A không vuông góc với BC.
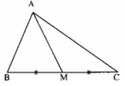
Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử AM ⊥ BC. Khi đó AM là đường trung trực của đoạn thẳng BC. Suy ra AB = AC. Điều này mâu thuẫn với giả thiết AB ≠ AC. Vậy trung tuyến AM không vuông góc với BC.
Chứng minh rằng nếu trong tam giác ABC có hai cạnh AB và AC không bằng nhau thì đường trung tuyến xuất phát từ đỉnh A không vuông góc với BC
Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử AM ⊥ BC. Khi đó AM là đường trung trực của đoạn thẳng BC.
Suy ra AB = AC. Điều này mâu thuẫn với giả thiết AB ≠ AC. Vậy trung tuyến AM không vuông góc với BC.

Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử AM ⊥ BC. Khi đó AM là đường trung trực của đoạn thẳng BC. Suy ra AB = AC. Điều này mâu thuẫn với giả thiết AB ≠ AC. Vậy trung tuyến AM không vuông góc với BC.