giá trị của biểu thức x^3+y^3 biết x + y =3 ;x^2 +y^2=13

Những câu hỏi liên quan
Tính giá trị của biểu thức sau, biết x+y=0
M=x^4-xy^3+x^3y-y^4-1=0
tính giá trị của biểu thức sau, biết x+y+1=0
D=X^2(x+y)-y^2 (x+y)+x^2-y^2+2(x+y)+3
Cho biểu thức
x
-
3
+
y
-
4
biết x + y 8. Giá trị lớn nhất của biểu thức là ? A. 1 B.
2
C.
3
D.
5
Đọc tiếp
Cho biểu thức x - 3 + y - 4 biết x + y = 8. Giá trị lớn nhất của biểu thức là ?
A. 1
B. 2
C. 3
D. 5
Chọn đáp án B.
Áp dụng BĐT Bunhia – copxki ta có:
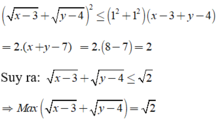
Đúng 0
Bình luận (0)
a, Giá trị nhỏ nhất của A= -x^2+x+1
b, Giá trị của biểu thức : x^3 + y^3 biết x+y=3 và x^2+y^2 = 13
tính giá trị của biểu thức biết x+y=2
M= 3(x^2+y^2)-(x^3+y^3)+1
Ta có :
\(M=3\left(x^2+y^2\right)-\left(x^3+y^3\right)+1\)
\(=3\left(x^2+y^2+2xy-2xy\right)-\left(x+y\right)\left(x^2+y^2-xy\right)+1\)
\(=3\left(x^2+y^2+2xy\right)-6xy-\left(x+y\right)\left(x^2+y^2+2xy-3xy\right)+1\)
\(=3.\left(x+y\right)^2-6xy-\left[\left(x+y\right)\left(x^2+y^2+2xy\right)-\left(x+y\right)3xy\right]+1\)
\(=3\left(x+y\right)^2-6xy-\left(x+y\right)\left(x+y\right)^2+\left(x+y\right)3xy+1\)
\(=3\left(x+y\right)^2-6xy-\left(x+y\right)^3+\left(x+y\right)3xy+1\)
Thay \(x+y=2;\)có :
\(M=3.2^2-6xy-2^3+6xy+1\)
\(=12-8+1\)
\(=5\)
Vậy ...
Đúng 0
Bình luận (0)
biết x-y =2 tính giá trị của biểu thức x^3- y^3 - 6xy
Ta có: x3- y3- 6xy = (x-y)( x2+ xy+y2 ) - 6xy
= 2( x2+ xy+ y2 )-2.3xy
= 2( x2+ xy+ y2 -3xy)
= 2( x2+ 2xy+ y2 )
= 2( x+ y )2
= 2. 22 = 8
Đúng 0
Bình luận (1)
x3-y3-6xy = (x-y)(x2+xy+y2)-6xy
Thay x-y = 2,ta có:
2(x2+xy+y2)-6xy=2(x2+xy+y2-3xy)=2(x2-2xy+y2)=2(x-y)2=
Thay x-y =2, ta có:
2.22=2.4=8
Đúng 0
Bình luận (0)
1.Tính giá trị của biểu thức: A=6x3−3x2+2|x|+4A=6x3−3x2+2|x|+4 với x=−23
2.Tính giá trị của biểu thức: B=2|x|−3|y|B=2|x|−3|y| với x=12;y=−3x=12;y=−3.
3.Tìm x, biết: |2 + 3x| = |4x - 3|
1. A = 6x^3 - 3x^2 + 2.|x| + 4 với x = -23
Thay x = -23 vào biểu thức trên, ta có:
A = 6.(-23)^3 - 3.(-23)^2 + 2.|-23| + 4
A = -74539
2. B = 2.|x| - 3.|y| với x = 12; y = -3
Thay x = 12; y = -3 vào biểu thức trên, ta có:
B = 2.|12| - 3.|-3|
B = 15
3. |2 + 3x| = |4x - 3|
ta có: 2 + 3x = \(\hept{\begin{cases}4x-3\Leftrightarrow4x-3\ge0\Leftrightarrow x\ge\frac{3}{4}\\-\left(4x-3\right)\Leftrightarrow4x-3< 0\Leftrightarrow x< \frac{3}{4}\end{cases}}\)
Nếu x >= 3/4, ta có phương trình:
2 + 3x = 4x - 3
<=> 3x - 4x = -3 - 2
<=> -x = 5
<=> x = 5 (TM)
Nếu x < 3/4, ta có phương trình:
2 + 3x = -(4x - 3)
<=> 2 + 3x = -4x + 3
<=> 3x + 4x = 3 - 2
<=> 7x = 1
<=> x = 1/7 (TM)
Vậy: tập nghiệm của phương trình là: S = {5; 1/7}
Tìm giá trị nhỏ nhất của biểu thức : A=x^3+y^3+xy biết x,y thỏa mãn: x+y=1
\(x+y=1\Rightarrow x=1-y\)
\(A=x^3+y^3+xy\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(=x^2+y^2\) (vì x + y = 1)
\(=\left(1-y\right)^2+y^2\)
\(=2y^2-2y+1\)
\(=2\left(y^2-y+\frac{1}{4}\right)+\frac{1}{2}=2\left(y-\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}\forall y\)
Dấu "=" xảy ra khi: \(y-\frac{1}{2}=0\Rightarrow y=\frac{1}{2}\Rightarrow x=1-y=\frac{1}{2}\)
Vậy GTNN của A là \(\frac{1}{2}\)khi \(x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
\(A=x^3+y^3+xy=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(=x^2-xy+y^2+xy=x^2+y^2\ge\frac{\left(x+y\right)^2}{2}=\frac{1}{2}\)
Nên min A là \(\frac{1}{2}\) khi \(x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
tính giá trị của biểu thức(x+y)^2 biết x-y=5,xy=3
$(x+y)^2\\=x^2+2xy+y^2\\=(x^2-2xy+y^2)+4xy\\=(x-y)^2+4xy\\=5^2+4.3\\=25+12\\=37$
Đúng 0
Bình luận (0)
`A=(x+y)^2=x^2+2xy+y^2=(x^2-2xy+y^2)+4xy=(x-y)^2+4xy`
Thay `x-y=5;xy=3` được: `A=5^2+4.3=37`
Đúng 0
Bình luận (0)
giá trị của biểu thức 2(x3-y3)-3(x+y)2 biết x-y=2
giá trị của biểu thức A= (3^(x+y)^2)/ (3^(x-y)^2) biết xy= 1/2






















