Bài hay quá!

Điểm cách đều tam giác ở đây chắc là tâm đường tròn nội tiếp?

Gọi điểm tiếp xúc của đường tròn nội tiếp (O) với hai cạnh BC,AB là D,F. Gọi M là trung điểm của BC và phân giác AO cắt đường tròn ngoại tiếp tam giác ABC ở K.

Ta kí hiệu \(a,b,c\) là độ dài ba cạnh BC,CA,AB như thông thường. Ta có ngay \(b+c=2a,\)(do giả thiết). Mặt khác \(AF=\frac{b+c-a}{2}=\frac{a}{2}=BM\).  Mặt khác \(\angle MBK=\frac{\angle A}{2}=\angle FAO\). Suy ra \(\Delta FAO=\Delta MBK\) (cạnh huyền, cạnh góc vuông). Do vậy \(\text{AO=BK, FO=KM}\), suy ra \(OD=KM\). . Gọi \(T=AK\cap BC\) suy ra \(T\) là trung điểm \(KO\). 

Cuối cùng để ý rằng \(\angle OBK=\frac{B}{2}+\frac{A}{2}=\angle BOK\to\Delta OBK\) cân ở \(K\), do đó \(KB=KO=KA\to AO=2OT.\) Vậy ta có \(\frac{AO}{OT}=2=\frac{AG}{GN}\to\) theo định lý Ta-let đảo thì OG song song BC.
 

Bài này hay đến nỗi nên thơ, hay đến nỗi nỗi làm rung động các nhà bác học  toán lừng danh trên thế giới

                                         Em ngồi bật olm

                          Lúc vào giải toán thấy câu hỏi này

                                 Em ngồi suy nghĩ chần chừ

                                 Tìm ra đáp số thế mà lại sai   

                                Bài này công nhận là hay

                             Vừa hay vừa khó quả là đỉnh cao   

                                Bạn nào thấy bài thơ đây 

                            Vui lòng các bạn cho mình ****

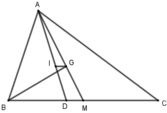
Gọi D, M là giao điểm của AI, AG với BC.

Vì AD là tia phân giác góc B A C ^  nên B D A B = D C A C  (t/c)

⇒ B D 12 = D C 18 = B D + D C 12 + 18 = 15 30 = 1 2

=> BD = 12. 1 2  = 6, DC =18. 1 2  = 9

Lại có: BI là tia phân giác A B D ^ nên A I I D = A B B D = 12 6 = 2  (tính chất)

=> I D A D = M G M A = 1 3  hay D đúng

Mà AG = 2GM (vì G là trọng tâm)

Nên A I I D = A G G M = 2  hay B đúng

Theo định lí đảo của định lí Talet ta có:

IG // DM => IG // BC hay A đúng

Chỉ có C sai

Đáp án: C

Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,

ghghhggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggghhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh

a: OM//AH

ON//BH

MN//AB

=>góc BAH=góc OMN và góc ABH=góc ONM

=>ΔABH đồng dạng vơi ΔMNO

b: G là trọng tâm của ΔABC

=>GM/GA=1/2

ΔABH đồng dạng với ΔMNO nên OM/AH=MN/AB=1/2

=>OM/AH=MG/AG

=>ΔHAG đồng dạng với ΔOMG

c: ΔHAG đồng dạng với ΔOMG

=>góc AGH=góc OGM và GH/GO=GA/GM=2

=>H,G,O thẳng hàng và GH=2GO

a: OM//AH

ON//BH

MN//AB

=>góc BAH=góc OMN và góc ABH=góc ONM

=>ΔABH đồng dạng với ΔMNO

b: A,G,M thẳng hàng và H,G,O thẳng hàng

=>góc AGH=góc MGO

=>ΔAHG đồng dạng với ΔMOG

=>OM/AH=MG/AG

=>OM/AH=MN/AB=1/2

=>GM/GA=1/2

=>G là trọng tâm của ΔACB