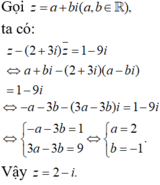Tìm số phức \(z\), biết : \(z-\left(2+3i\right)\overline{z}=1-9i\)

Những câu hỏi liên quan
Bài tập số 4: Tìm số phức liên hợp overline{Z} và tính modun (|z|) của số phức sau. a, z 2 + 3i b, zleft(2+3iright)^3 c, zdfrac{2+3i}{1-2i} d, zsqrt{2}-dfrac{4}{3}i
Đọc tiếp
Bài tập số 4: Tìm số phức liên hợp \(\overline{Z}\) và tính modun (|z|) của số phức sau.
a, z = 2 + 3i b, \(z=\left(2+3i\right)^3\)
c, \(z=\dfrac{2+3i}{1-2i}\) d, \(z=\sqrt{2}-\dfrac{4}{3}i\)
Tìm tất cả các số phức \(z\) thỏa mãn điều kiện:
\(\left|iz-1-3i\right|.\left|\overline{z}+1+i\right|=\left|z^2+\left(-6+2i\right)z+8-6i\right|\) và \(\dfrac{z-3}{z+2}\) là số thuần ảo.
Tìm số phức z, biết
z
-
(
2
+
3
i
)
z
¯
1
-
9
i
Đọc tiếp
Tìm số phức z, biết z - ( 2 + 3 i ) z ¯ = 1 - 9 i
![]()
![]()
![]()
![]()
Tìm mô đun của số phức z, biết
z
-
(
2
+
3
i
)
z
¯
-
17
+
9
i
A. . B. . C.. D. .
Đọc tiếp
Tìm mô đun của số phức z, biết z - ( 2 + 3 i ) z ¯ = - 17 + 9 i
A. ![]() .
.
B. ![]() .
.
C.![]() .
.
D. ![]() .
.
Cho số phức z thỏa mãn \(\left(1+i\right)z+2\overline{z}=2\)
Tính môdun của số phức \(\omega=z+2+3i\)
Giả sử: \(z=x+yi\) \((x;y\in|R)\)
Ta có: \((1+i)z+2\overline{z}=2\)
<=> \((1+i)(x+yi)+2(x-yi)=2\)
<=> \(x+yi+xi-y+2x-2yi-2=0\)
<=> \((3x-y-2)+(x-y)i=0\)
<=> \(\begin{align} \begin{cases} 3x-y&=2\\ x-y&=0 \end{cases} \end{align}\)
<=> \(\begin{align} \begin{cases} x&=1\\ y&=1 \end{cases} \end{align}\)
=> \(z=1+i\)
Ta có: \(\omega=z+2+3i \)
\(=1+i+2+3i\)
\(=3+4i\)
=> \(|\omega|=\sqrt{3^2+4^2}=5\)
Đúng 0
Bình luận (0)
Đặt \(z=a+bi\left(a,b\in R\right)\)
Theo bài ta có : \(\begin{cases}3a-b=2\\a-b=0\end{cases}\) \(\Leftrightarrow\begin{cases}a=1\\b=1\end{cases}\) nên \(z=1+i\)
Khi đó \(\omega=z+2+3i=1+i+2+3i=3+4i\)
Vậy \(\left|\omega\right|=\sqrt{3^2+4^2}=5\)
Đúng 0
Bình luận (0)
Cho N là điểm biểu diễn số phức z thỏa mãn \(\dfrac{z+2-3i}{z-3}=1-i\) và M là điểm biểu diễn số phức z' thoả mãn \(\left|z'-2-i\right|+\left|z'+3-3i\right|=\sqrt{29}\). Tìm giá trị nhỏ nhất của MN
1. Cho số phức z thỏa mãn hệ thức | z-1+i | | z-2-3i |. Tìm giá trị nhỏ nhất của biểu thức P | z+2+i | + | z-3+2i |
2. Cho số phức z thỏa mãn hệ thức | z-i | 2. Biết rằng | z | lớn nhất. Tìm phần ảo của z
3. Cho số phức z thỏa overline{z}left(i+sqrt{2}right)^2left(1-sqrt{2}iright). Tìm phần ảo của số phức z
4. Cho 2 số phức z m + 3i, z 2 - (m + 1)i. Tìm giá trị thực của m để z.z là số thực
5. Cho 3 điểm A, B, M lần lượt biểu diễn các số phức -4, 4i, x + 3i. Với giá trị thực nào của x th...
Đọc tiếp
1. Cho số phức z thỏa mãn hệ thức | z-1+i | = | z-2-3i |. Tìm giá trị nhỏ nhất của biểu thức P = | z+2+i | + | z-3+2i |
2. Cho số phức z thỏa mãn hệ thức | z-i | = 2. Biết rằng | z | lớn nhất. Tìm phần ảo của z
3. Cho số phức z thỏa \(\overline{z}=\left(i+\sqrt{2}\right)^2\left(1-\sqrt{2}i\right)\). Tìm phần ảo của số phức z
4. Cho 2 số phức z = m + 3i, z' = 2 - (m + 1)i. Tìm giá trị thực của m để z.z' là số thực
5. Cho 3 điểm A, B, M lần lượt biểu diễn các số phức -4, 4i, x + 3i. Với giá trị thực nào của x thì A, B, M thẳng hàng?
6. Cho 2 số phức \(z_1=1+2i\), \(z_2=2-3i\). Xác định phần ảo của số phức \(3z_1-2z_2\)
7. Nếu mô đun số phức z bằng m thì mô đun của số phức \(\left(1-i\right)^2z\) bằng?
8. Trong tất cả các số phức z thỏa mãn hệ thức | z-1+3i | = 3. Tìm min | z-1-i |
9. Trong mặt phẳng phức tìm điểm biểu diễn số phức z = \(\frac{i^{2017}}{3+4i}\)
10. Trong mặt phẳng phức với hệ trục tọa độ Oxy, điểm biểu diễn của các số phức z = 3 + bi với b \(\in\) R luôn nằm trên đường có phương trình là: A. y = x B. x = 3 C. y = x + 3 D. y = 3
11. Cho 2 số phức \(z_1=1+2i\), \(z_2=2-3i\). Tổng hai số phức là?
12. Cho số phức z = 2 + 5i. Tìm số phức \(w=iz+\overline{z}\)
13. Ký hiệu \(z_0\) là nghiệm phức có phần ảo âm của phương trình \(z^2+z+1=0\). Tìm trên mặt phẳng tọa độ điểm nào dưới đây là điểm biểu diễn số phức \(w=\frac{i}{z_0}\): A. \(M\left(-\frac{\sqrt{3}}{2};-\frac{1}{2}\right)\) B. \(M\left(-\frac{\sqrt{3}}{2};\frac{1}{2}\right)\) C. \(M\left(\frac{\sqrt{3}}{2};-\frac{1}{2}\right)\) D. \(M\left(-\frac{1}{2};-\frac{\sqrt{3}}{2}\right)\)
14. Cho số phức z thỏa mãn hệ thức | z+7-5i | = | z-1-11i |. Biết rằng số phức z = x + yi thỏa mãn \(\left|z-2-8i\right|^2+\left|z-6-6i\right|^2\) đạt giá trị nhỏ nhất. Giá trị của biểu thức \(p=x^2-y^2\)?
15. Gọi \(z_0\) là nghiệm phức có phần ảo âm của phương trình \(2z^2-6z+5=0\). Điểm nào sau đây biểu diễn số phức \(iz_0\): A. \(M\left(\frac{3}{2};\frac{1}{2}\right)\) B. \(M\left(\frac{3}{2};-\frac{1}{2}\right)\) C. \(M\left(-\frac{1}{2};\frac{3}{2}\right)\) D. \(M\left(\frac{1}{2};\frac{3}{2}\right)\)
16. Tính mô đun của số phức \(w=z^2+i\overline{z}\) biết z thỏa mãn \(\left(1+2i\right)z+\left(2+3i\right)\overline{z}=6+2i\)
17. Trong mặt phẳng phức, cho 3 điểm A, B, C lần lượt biểu diễn 3 số phức \(z_1=1+i\), \(z_2=\left(1+i\right)^2\), \(z_3=a-i\left(a\in R\right)\). Để tam giác ABC vuông tại B thì A bằng? A. -3 B. 3 C. -4 D. -2
18. Cho số phức z thỏa mãn (1+2i)z = 3+i. Tính giá trị biểu thức \(\left|z\right|^4-\left|z\right|^2+1\)
19. Cho số phức z = a + (a-1)i (a\(\in R\)). Giá trị thực nào của a để | z | = 1 ?
20. Cho số phức z thoả mãn hệ thức | z+5-i | = | z+1-7i |. Tìm giá trị lớn nhất của biểu thức P = | |z-4-i| - |z-2-4i| |
21. Trong các số phức z = a + bi thỏa mãn | z-1+2i | =1, biết rằng | z+3-i | đạt giá trị nhỏ nhất. Tính \(p=\frac{a}{b}\)
22. Gọi A, B, C lần lượt là các điểm biểu diễn các số phức \(z_1=-1+3i\), \(z_2=-3-2i\), \(z_3=4+i\). Chọn kết luận đúng nhất: A. Tam giác ABC cân B. Tam giác ABC đều C. Tam giác ABC vuông D. Tam giác ABC vuông cân
23. Cho số phức z = 5-3i. Tính \(1+\overline{z}+\left(\overline{z}\right)^2\)
24. Cho \(f\left(z\right)=z^3-3z^2+z-1\) với z là số phức. Tính \(f\left(z_0\right)-f\left(\overline{z_0}\right)\) biết \(z_0=1-2i\)
25. Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M (3;-4) là: A. \(\sqrt{13}\) B. \(2\sqrt{2}\) C. \(2\sqrt{5}\) D. \(2\sqrt{10}\)
Câu 1:
Gọi \(A\left(1;-1\right)\) và \(B\left(2;3\right)\Rightarrow\) tập hợp \(z\) thoả mãn điều kiện đề bài là đường trung trực d của đoạn AB, ta dễ dàng viết được phương trình d có dạng \(4x-y-5=0\)
Gọi \(M\left(-2;-1\right)\) và \(N\left(3;-2\right)\) và \(I\left(a;b\right)\) là điểm bất kì biểu diễn \(z\Rightarrow I\in d\) \(\Rightarrow P=IM+IN\). Bài toán trở thành dạng cực trị hình học phẳng quen thuộc: cho đường thẳng d và 2 điểm M, N cố định, tìm I thuộc d để \(P=IM+IN\) đạt GTNN
Thay toạ độ M, N vào pt d ta được 2 giá trị trái dấu \(\Rightarrow M;N\) nằm về 2 phía so với d
Gọi \(C\) là điểm đối xứng M qua d \(\Rightarrow IM+IN=IC+IN\), mà \(IC+IN\ge CN\Rightarrow P_{min}=CN\) khi I, C, N thẳng hàng
Phương trình đường thẳng d' qua M và vuông góc d có dạng:
\(1\left(x+2\right)+4\left(y+1\right)=0\Leftrightarrow x+4y+6=0\)
Gọi D là giao điểm d và d' \(\Rightarrow\left\{{}\begin{matrix}x+4y+6=0\\4x-y-5=0\end{matrix}\right.\) \(\Rightarrow D\left(\frac{14}{17};-\frac{29}{17}\right)\)
\(\overrightarrow{MD}=\overrightarrow{DC}\Rightarrow C\left(-2;-1\right)\Rightarrow P_{min}=CN=\sqrt{\left(3+2\right)^2+\left(-2+1\right)^2}=\sqrt{26}\)
Bài 2:
Tập hợp \(z\) là các điểm M thuộc đường tròn (C) tâm \(I\left(0;1\right)\) bán kính \(R=\sqrt{2}\) có phương trình \(x^2+\left(y-1\right)^2=2\)
\(\Rightarrow\left|z\right|=OM\Rightarrow\left|z\right|_{max}\) khi và chỉ khi \(M;I;O\) thẳng hàng và M, O nằm về hai phía so với I
\(\Rightarrow M\) là giao điểm của (C) với Oy \(\Rightarrow M\left(0;1+\sqrt{2}\right)\Rightarrow\) phần ảo của z là \(b=1+\sqrt{2}\)
Câu 3:
\(\overline{z}=\left(i+\sqrt{2}\right)^2\left(1-\sqrt{2}i\right)=5+\sqrt{2}i\)
\(\Rightarrow z=5-\sqrt{2}i\Rightarrow b=-\sqrt{2}\)
Đúng 0
Bình luận (0)
Câu 4
\(z.z'=\left(m+3i\right)\left(2-\left(m+1\right)i\right)=2m-\left(m^2+m\right)i+6i+3m+3\)
\(=5m+3-\left(m^2+m-6\right)i\)
Để \(z.z'\) là số thực \(\Leftrightarrow m^2+m-6=0\Rightarrow\left[{}\begin{matrix}m=2\\m=-3\end{matrix}\right.\)
Câu 5:
\(A\left(-4;0\right);B\left(0;4\right);M\left(x;3\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(4;4\right)\\\overrightarrow{AM}=\left(x+4;3\right)\end{matrix}\right.\) \(\Rightarrow A,B,M\) khi và chỉ khi \(\frac{x+4}{4}=\frac{3}{4}\Rightarrow x=-1\)
Câu 6:
\(z=3z_1-2z_2=3\left(1+2i\right)-2\left(2-3i\right)=-1+12i\)
\(\Rightarrow b=12\)
Câu 7:
\(w=\left(1-i\right)^2z\)
Lấy môđun 2 vế:
\(\left|w\right|=\left|\left(1-i\right)^2\right|.\left|z\right|=2m\)
Câu 8:
\(3=\left|z-1+3i\right|=\left|z-1-i+4i\right|\ge\left|\left|z-1-i\right|-\left|4i\right|\right|=\left|\left|z-1-i\right|-4\right|\)
\(\Rightarrow\left|z-1-i\right|\ge-3+4=1\)
Đúng 0
Bình luận (2)
Câu 9:
\(z=\frac{i^{2017}}{3+4i}=\frac{\left(i^2\right)^{1008}.i}{3+4i}=\frac{i}{3+4i}=\frac{i\left(3-4i\right)}{\left(3-4i\right)\left(3+4i\right)}=\frac{4}{25}+\frac{3}{25}i\)
Điểm biểu diễn z là \(A\left(\frac{4}{25};\frac{3}{25}\right)\)
Câu 10:
\(a=3\Rightarrow z\) nằm trên đường thẳng \(x=3\)
Câu 11:
\(z_1+z_2=1+2i+2-3i=3-i\)
Câu 12:
\(z=2+5i\Rightarrow\overline{z}=2-5i\)
\(\Rightarrow w=i\left(2+5i\right)+2-5i=-3-3i\)
Câu 13:
\(z^2+z+1=0\Rightarrow\left\{{}\begin{matrix}z_1=-\frac{1}{2}+\frac{\sqrt{3}}{2}i\\z_2=-\frac{1}{2}-\frac{\sqrt{3}}{2}i\end{matrix}\right.\) (ném vô casio cho giải pt)
\(\Rightarrow z_0=-\frac{1}{2}-\frac{\sqrt{3}}{2}i\Rightarrow w=\frac{i}{z_0}=-\frac{\sqrt{3}}{2}-\frac{1}{2}i\) (ném vô mode 2 bấm cho lẹ) \(\Rightarrow M\left(-\frac{\sqrt{3}}{2};-\frac{1}{2}\right)\)
Câu 14:
Đặt \(z=x+yi\) \(\Rightarrow\left|x+7+\left(y-5\right)i\right|=\left|x-1+\left(y-11\right)i\right|\)
\(\Rightarrow\left(x+7\right)^2+\left(y-5\right)^2=\left(x-1\right)^2+\left(y-11\right)^2\)
\(\Rightarrow4x+3y-12=0\) quỹ đạo là đường thẳng d
Gọi \(A\left(2;8\right);B\left(6;6\right)\) và I là trung điểm AB \(\Rightarrow I\left(4;7\right)\)
\(M\left(x;y\right)\) là điểm biểu diễn \(z\Rightarrow P=MA^2+MB^2\)
Tam giác AMB có MI là trung tuyến ứng với cạnh AB
Theo công thức trung tuyến: \(MA^2+MB^2=2MI^2+\frac{AB^2}{2}\)
\(\Rightarrow P_{min}\) khi và chỉ khi \(MI_{min}\)
Gọi \(C\) là hình chiếu của I lên d \(\Rightarrow\Delta ICM\) vuông tại C, do IM là cạnh huyền và IC là cạnh góc vuông nên \(IM\ge IC\Rightarrow IM_{min}=IC\)
Vậy ta quy về bài toán tìm hình chiếu của I lên d
Đường thẳng qua I vuông góc với d có pt:
\(3\left(x-4\right)-4\left(y-7\right)=0\Leftrightarrow3x-4y+16=0\)
Tọa độ C là nghiệm: \(\left\{{}\begin{matrix}4x+3y-12=0\\3x-4y+16=0\end{matrix}\right.\) \(\Rightarrow C\left(0;4\right)\)
\(\Rightarrow p=x^2-y^2=0^2-4^2=-16\) (p này khác P kia nha :D)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho số phức z thoa mãn (1+2i)z+(1+2\(\overline{z}\))i=1+3i tìm moodun cua z
Z= a+bi và \(\overline{Z}\) =a-bi → (1+2i).(a+bi) +(1+2a-2bi)i =1+3i
→a+bi +2ai -2b +i +2ai +2b=1+3i (i2= -1)
→ a+ (4a+b+1)i = 1+3i
→\(\begin{cases}a=1\\4a+b+1=3\end{cases}\) → a=1 , b=-2 → modum : \(\left|Z\right|\)=\(\sqrt{5}\)
Đúng 0
Bình luận (0)
Tìm số phức z thỏa mãn \(\frac{\left(\left|z\right|-1\right)\left(1+iz\right)}{z-\frac{1}{\overline{z}}}=i\)
Điều kiện \(z\ne0;\left|z\right|\ne1\)
\(\Leftrightarrow\frac{\overline{z}\left(\left|z\right|-1\right)\left(1+iz\right)}{\left|z\right|^2-1}=i\Leftrightarrow\frac{\overline{z}\left(\left|z\right|-1\right)\left(1+iz\right)}{\left(\left|z\right|-1\right)\left(\left|z\right|+1\right)}\)
\(\Leftrightarrow\overline{z}\left(1+iz\right)=\left(\left|z\right|+1\right)i\)
\(\Leftrightarrow\overline{z}+i\left|z\right|^2=\left(\left|z\right|+1\right)i\) (*)
Giả sử \(z=x+yi,x,y\in R\), khi đó (*) trở thành :
\(x-yi+\left(x^2+y^2\right)i=\left(\sqrt{x^2+y^2}+1\right)i\)
\(\Leftrightarrow x+\left(x^2+y^2-\sqrt{x^2+y^2}-y-1\right)i=0\)
\(\Leftrightarrow\begin{cases}x=0\\x^2+y^2-\sqrt{x^2+y^2}-y-1=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=0\\y^2-\left|y\right|-y-1=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=0\\\begin{cases}y=-1\\y=1+\sqrt{2}\end{cases}\end{cases}\)
Nếu \(x=0,y=1+\sqrt{2}\) thì \(z=\left(1+\sqrt{2}\right)i\) thỏa mãn điều kiện
Nếu \(x=0,y=-1\) thì \(z=-i\) , khi đó \(\left|z\right|=1\) không thỏa mãn điều kiện
Vậy số phức cần tìm là \(z=\left(1+\sqrt{2}\right)i\)
Đúng 0
Bình luận (0)