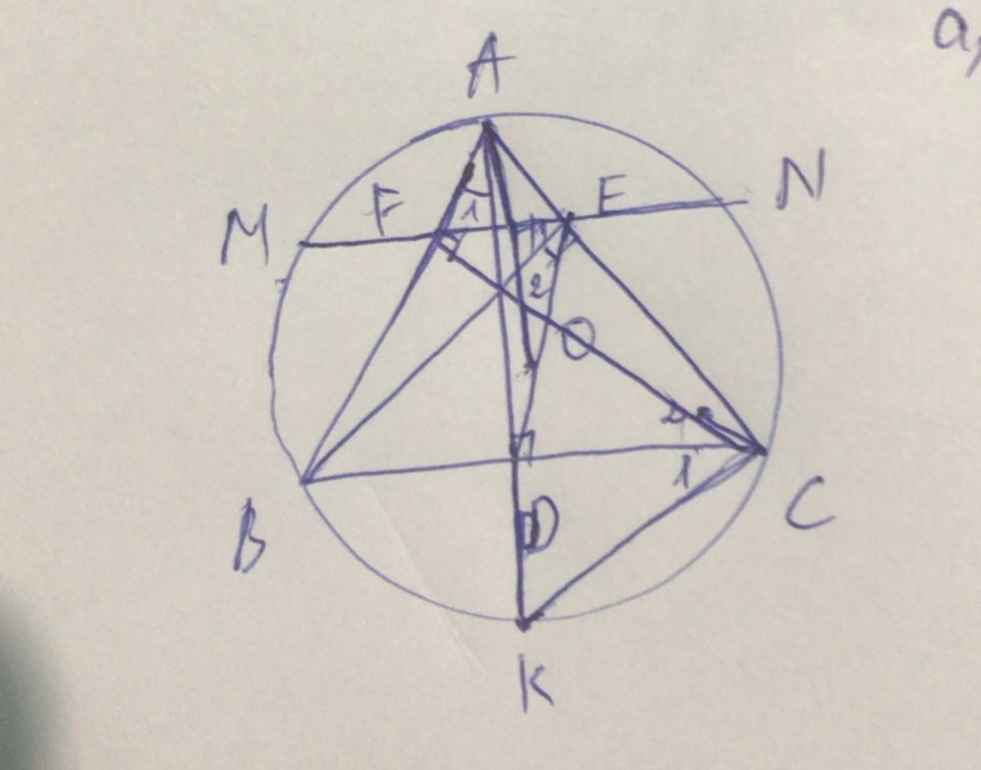
Cho tam giác ABC nhọn có hai đường cao BE,CF. Các điểm M,N,L theo thứ tự là trung điểm của BF,CE,EF. Đường thẳng qua M vuông góc với BL và đường thẳng qua N vuông góc với CL cắt nhau tại K. Chứng minh rằng KB=KC.

Những câu hỏi liên quan
Cho tam giác nhọn ABC có ABAC, các đường cao AD, BE, CF cắt nhau tại H. ĐƯờng thẳng đi qua C và vuông góc với AC cắt đường thẳng đi qua B và vuông góc với AB tại điểm K. Gọi M là trung điểm của BC, I là trung điểm của AKa) CHứng minh: BECF và IMdfrac{1}{2}AHb) Gọi G là trọng tâm của tam giác ABC. CHứng minh: 3 điểm H, G, I thẳng hàng. c) CM: dfrac{HD}{AD}+dfrac{HE}{BE}+dfrac{HF}{CF}1
Đọc tiếp
Cho tam giác nhọn ABC có AB<AC, các đường cao AD, BE, CF cắt nhau tại H. ĐƯờng thẳng đi qua C và vuông góc với AC cắt đường thẳng đi qua B và vuông góc với AB tại điểm K. Gọi M là trung điểm của BC, I là trung điểm của AK
a) CHứng minh: BE<CF và \(IM=\dfrac{1}{2}AH\)
b) Gọi G là trọng tâm của tam giác ABC. CHứng minh: 3 điểm H, G, I thẳng hàng.
c) CM: \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=1\)
a) Ta có:
\(\left\{{}\begin{matrix}BH\perp AC\\KC\perp AC\end{matrix}\right.\) ⇒ \(BH\text{//}KC\)
\(\left\{{}\begin{matrix}CH\perp AB\\BK\perp AB\end{matrix}\right.\) ⇒ \(CH\text{//}BK\)
\(Xét\) \(tứ\) \(giác\) \(BKCH\) \(có:\) \(\left\{{}\begin{matrix}BH\text{//}KC\\CH\text{//}BK\end{matrix}\right.\)
⇒ Tứ giác \(BKCH\) là hình hình hành. Mà M là trung điểm của đường chéo BC
⇒ \(\left\{{}\begin{matrix}H,M,K_{ }thẳng_{ }hàng\\HM=MK\end{matrix}\right.\)
Xét \(\Delta AHK\) có: \(\left\{{}\begin{matrix}AI=IK\left(gt\right)\\HM=MK\left(cmt\right)\end{matrix}\right.\)
⇒ \(IM\) là đường trung bình của \(\Delta AHK\)
⇒ \(IM=\dfrac{1}{2}AH\) \(\left(ĐPCM\right)\)
c)
Ta có:
\(\dfrac{S_{\Delta HBC}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HD.BC}{\dfrac{1}{2}.AD.BC}=\dfrac{HD}{AD}\)
\(\dfrac{S_{\Delta HAC}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HE.AC}{\dfrac{1}{2}.BE.AC}=\dfrac{HE}{BE}\)
\(\dfrac{S_{\Delta HBA}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HF.AB}{\dfrac{1}{2}.CF.AB}=\dfrac{HF}{CF}\)
⇒ \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=\dfrac{S_{\Delta HBC}+S_{\Delta HAC}+S_{\Delta HAB}}{S_{\Delta ABC}}=\dfrac{S_{\Delta ABC}}{S_{\Delta ABC}}\)
⇔ \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=1\) \(\left(ĐPCM\right)\)
Đúng 3
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn, các đường cao BD và CE cắt nhau tại H. Qua B kẻ đường thẳng vuông góc với Ab tại B, qua C kẻ đường thẳng vuông góc với AC tại C, chúng cắt nhau tại K. Gọi M là trung điểm của BC
a) Chứng minh: H, M, K thẳng hàng
b) Tam giác ABC thỏa mãn điều kiện gì để tứ giác BHCK là hình thoi
c) Gọi O là trung điểm của AK, CH giao với MA tại G. Chứng minh: G là trọng tâm của tam giác ABC
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn, các đường cao BD và CE cắt nhau tại H. Qua B kẻ đường thẳng vuông góc với Ab tại B, qua C kẻ đường thẳng vuông góc với AC tại C, chúng cắt nhau tại K. Gọi M là trung điểm của BC
a) Chứng minh: H, M, K thẳng hàng
b) Tam giác ABC thỏa mãn điều kiện gì để tứ giác BHCK là hình thoi
c) Gọi O là trung điểm của AK, CH giao với MA tại G. Chứng minh: G là trọng tâm của tam giác ABC
a: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>H,M,K thẳng hàng
b: BHCK là hình thoi khi BH=HC
=>AB=AC
Đúng 0
Bình luận (0)
cho tam giác nhọn abc nội tiếp đường tròn (o).các đường cao ad,be,cf cắt nhau tại h.ad kéo dài cắt nhau tại điểm k(k khác a).đường thẳng ef cắt (o) tại m và n(f nằm giữa e và m). a,chứng minh d là trung điểm của hk. b,chứng minh oa vuông góc với mn. c,chứng minh am là tiếp tuyến của đường tròn ngoại tiếp tam giác mdh.
cho tam giác ABC nhọn (AB < AC), các đường cao AE,BF cắt nhau tại H. gọi M là trung điểm của BC, qua H vẽ đường thẳngA vuông góc với HM, a cắt AB,AC lần lượt tại I ,K. Qua C kẻ đường thẳng b song song với đường thẳng IK, b cắt AH,AB theo thứ tự tại N và D. chứng minh NC=ND,HI=HK
Cho tam giác ABC nhọn, đường cao AH. ĐIểm M thuộc BC. ĐƯờng thẳng qua A vuông góc với AM theo thứ tự cắt các đường thẳng qua M vuông góc với AB và AC tại E và F. CMR AH, BF,CE đồng quy.
Gọi BF,CE cắt nhau tại K và cắt AC,AB lần lượt tại S,T. Đường thẳng AH cắt MF,ME lần lượt tại P,Q.
Ta dễ thấy P là trực tâm của \(\Delta\)MAC, suy ra CP // EA (Cùng vuông góc AM). Tương tự BQ // FA
Áp dụng ĐL Melelaus và ĐL Thales ta có:
\(\frac{\overline{KB}}{\overline{KF}}.\frac{\overline{TA}}{\overline{TB}}.\frac{\overline{EF}}{\overline{EA}}=1\Rightarrow\frac{\overline{TA}}{\overline{TB}}=\frac{\overline{KF}}{\overline{KB}}.\frac{\overline{EA}}{\overline{EF}}=\frac{\overline{AF}}{\overline{QB}}.\frac{\overline{EA}}{\overline{EF}}\)
\(\frac{\overline{KC}}{\overline{KE}}.\frac{\overline{SA}}{\overline{SC}}.\frac{\overline{FE}}{\overline{FA}}=1\Rightarrow\frac{\overline{SC}}{\overline{SA}}=\frac{\overline{KC}}{\overline{KE}}.\frac{\overline{FE}}{\overline{FA}}=\frac{\overline{CP}}{\overline{EA}}.\frac{\overline{FE}}{\overline{FA}}\)
Suy ra \(\frac{\overline{TA}}{\overline{TB}}.\frac{\overline{HB}}{\overline{HC}}.\frac{\overline{SC}}{\overline{SA}}=\frac{\overline{CP}}{\overline{QB}}.\frac{\overline{HB}}{\overline{HC}}=-\frac{\overline{HC}}{\overline{HB}}.\frac{\overline{HB}}{\overline{HC}}=-1\)
Áp dụng điều kiện đủ của ĐL Ceva ta thu được AH,BS,CT đồng quy hay AH,BF,CE đồng quy (đpcm).
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn , I là trung điểm BC , BD và CE là hai đường cao . Đường thẳng đi qua A vuông góc với IE cắt CE tại M , đường thẳng đi qua A vuông góc với ID cắt BD tại N . Gọi F và G là trung điểm của BM và CN , H là giao điểm của EF và GD . CHỨNG MINH AH VUÔNG GÓC VỚI ED
Cho tam giác ABC nhọn có 3 đường cao AD, BE, CF. Đường thẳng qua A vuông góc với AB, cắt BE tại M; đường thẳng qua A vuông góc với AC, cắt CF tại N. Gọi I là trung điểm của BC. CMR: AI vuông góc với MN.
Câu hỏi của Diệp Song Thiên - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo link này nhé!
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn , I là trung điểm của BC , BD và CE là 2 đường cao .Đường thẳng đi qua A vuông góc với IE cắt CE tại M , Đường thẳng đi qua A vuông góc với ID cắt BD tại N . Gọi F và G là trung điểm của MB và CN , H là giao điểm của EF và GD . CHỨNG MINH AH VUÔNG GÓC VỚI ED
AM giao I
tam giac EBC vuong => EI =IC => goc CEI = ECI
tam giac TEM dong dang tam giac TAE => TEM = TAE
IEC = TEM doi dinh
=> TAE=ICE
tt => IME = IBE => AEM dong dang CEB (g-g)
=> ty le thuc
=> EMB dong dang EAC
=> BME=CAE
tam giac EMB vuong => EF = FM => FME =FEM
FEM = CEH (dd)
=> EAC=HEC. => EH vuong goc vs AE
tt => DH vuong goc vs AE
=> H la truc tam cua AED
=> AH vuong goc ED
công minh nghĩ cả buổi tối. tích cho cái nhé
Đúng 0
Bình luận (0)
cho tam giác abc nhọn, không cân (ab< ac), các đường cao ad,be,cf cắt nhau tại trực tâm h . gọi m,i lần lượt là trung điểm của bc, ah. đường thẳng qua i vuông góc với am, cắt ef tại s. 1) chứng minh ie vuông góc với me. 2) chứng minh sa song song với bc. 3) gọi p,q lần lượt là giao điểm của si với be,cf.chứng minh i là trung điểm của pq.
\({}\)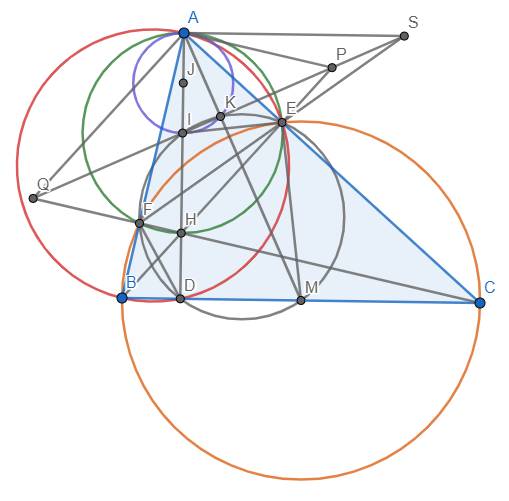
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)
Đúng 1
Bình luận (0)