\(\overrightarrow{AB}\left(2;2\right);\overrightarrow{AC}\left(2;-2\right)\)
\(\overrightarrow{AB}.\overrightarrow{AC}=2.2+2.\left(-2\right)=0\) nên \(AB\perp AC\). (1)
\(AB=\sqrt{2^2+2^2}=2\sqrt{2}\).
\(AC=\sqrt{2^2+\left(-2\right)^2}=2\sqrt{2}\)
Vì vậy AB = AC. (2)
Từ (1) và (2) suy ra tam giác ABC vuông cân tại A.

Chọn A.

Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.

B(4;5), C(-3;2)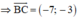 

Phương trình đường cao AH đi qua A(2;-1) nhận 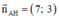 là VTPT là:

7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0

Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.

\(\overrightarrow{AB}=\left(4;-3\right)\Rightarrow AB=5\)

\(\overrightarrow{AC}=\left(6;0\right)\Rightarrow AC=6\)

\(\overrightarrow{BC}=\left(2;3\right)\Rightarrow BC=\sqrt{13}\)

Chu vi tam giác: \(AB+AC+BC=11+\sqrt{13}\)

vecto AH=(x+2;y-4); vecto BC=(-6;-2)

vecto BH=(x-4;y-1); vecto AC=(0;-5)

Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0

=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6

=>x+2=1 và y=1

=>x=-1 và y=1

\(\overrightarrow{AB}=\left(1;-2\right)\Rightarrow AB=\sqrt{5}\)

\(\overrightarrow{AC}=\left(-2;2\right)\Rightarrow AC=2\sqrt{2}\)

\(BC=\left(-3;4\right)\Rightarrow BC=5\)

Chu vi tam giác ABC: \(AB+AC+BC=\sqrt{5}+2\sqrt{2}+5\)

\(\left(x,y\right)\) là tâm đường tròn ngoại tiếp tam giác ABC

\(\Leftrightarrow\left\{{}\begin{matrix}IA=IB\\IA=IC\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}IA^2=IB^2\\IA^2=IC^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+1\right)^2+\left(y-2\right)^2=\left(x-2\right)^2+y^2\\\left(x+1\right)^2+\left(y-2\right)^2=\left(x+3\right)^2+\left(y-1\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}6x-4y=-1\\4x+2y=-5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{11}{14}\\y=-\dfrac{13}{14}\end{matrix}\right.\)

Vậy \(I\left(-\dfrac{11}{14};-\dfrac{13}{14}\right)\)

a) \(\cos A=-\dfrac{3}{5}\Rightarrow\widehat{A}\approx126^052'\)

b) \(AB:2x+y-1=0;AC=2x-y-3=0\)

c) Phân giác trong \(AD\) có phương trình : \(y+1=0\)

Gọi (C): x^2+y^2-2ax-2by+c=0 là PT đường tròn ngoại tiêpΔACB

Theo đề, ta có: 

2^2+(-1)^2-4a+2b+c=0 và 1+4+2a-4b+c=0 và 16+1+8a+2b+c=0

=>-4a+2b+c=-5 và 2a-4b+c=-5 và 8a+2b+c=-17

=>a=-1; b=-1; c=-7

=>x^2+y^2+2x+2y-7=0

=>x^2+2x+1+y^2+2y+1=9

=>(x+1)^2+(y+1)^2=9