chứng minh đường thẳng ơ le

Những câu hỏi liên quan
Giúp mình chứng minh đường thẳng Ơ-le bằng vecto vơi ?
GỌi H,G,O là trực tâm , trọng tâm và tâm đường tròn ngoại tiếp tam giác ABC , cần chứng minh H,G,O
Vẽ hình bình hành BHCK
\(\Rightarrow\hept{\begin{cases}\vec{HB}=\vec{CK}\\KC//BH\end{cases}}\)
\(\Rightarrow KC\perp AC\)
Xét tam giác ACK có \(\widehat{ACK}=90^o\Rightarrow\overline{A,O,K}\)(Do là đường kính)
Có \(\vec{HA}+\vec{HB}+\vec{HC}=2\vec{HO}\)
\(\Leftrightarrow3\vec{HG}+\vec{GA}+\vec{GB}+\vec{GC}=2\vec{HO}\)
\(\Leftrightarrow3\vec{HG}+\vec{0}=2\vec{HO}\)(Hệ thức trọng tâm)
\(\Rightarrow\vec{HG}=\frac{2}{3}\vec{HO}\)
\(\Rightarrow\overline{H,G,O}\left(Dpcm\right)\)
Đúng 0
Bình luận (0)

∆ABC có H là trực tâm, G là trọng tâm, O là giao điểm của 3 đường trung trực.
Gọi M là trung điểm của BC. Lấy D đối xứng với A qua O
Ta có: OA = OC (tính chất của điểm thuộc đường trung trực)
Mà OA = OD (theo cách chọn điểm phụ) nên OA = OC = OD
Do đó ∆ACD vuông tại C \(\Rightarrow CD\perp AC\)
Mà \(\Rightarrow BH\perp AC\left(gt\right)\Rightarrow BH//CD\)(1)
Chứng minh tương tự: \(CH//BD\)(2)
Từ (1) và (2) suy ra BHCD là hình bình hành có M là trung điểm của BC nên M cũng là trung điểm của HD (cũng suy ra được H, M, D thẳng hàng)
∆ADH có AM là trung tuyến và \(AG=\frac{2}{3}AM\left(gt\right)\)nên G là trọng tâm
\(\Rightarrow\)Trung tuyến thứ hai là HO đi qua G
Vậy H, G, O thẳng hàng
Bạn phía dưới làm đúng
Xem thêm câu trả lời
Hãy chứng minh định lí Ơ-le ?
Cho tam giác ABC có trực tâm H , trọng tâm G , O là tâm đường tròn
ngoại tiếp , I là trung điểm BC , AD là đường kính của (O) .
Chứng minh H , G , O thẳng hàng ?
Giải :
Ta có : góc DCA = góc DBA = 90 độ ( góc nội tiếp chắn 1/2 (O))
Xét tứ giác BHCD ta có :
BH // DC ( vì cùng vuông góc với AC )
CH // DB ( vì cùng vuông góc với AB )
Do đó tứ giác BHCD là hình bình hành .
===> H , I , D thẳng hàng và IH = ID (t/c đường chéo hbhành)
Ta lại có : OI = 1/2 AH ( đ.trung bình tam giác DAH ) (1)
GI = 1/2 GA (t/chất trọng tâm của ABC ) (2)
góc HAG = góc GIO ( so le trong vì AH // OI ) (3)
Do đó tam giác GAH đồng dạng tam giác GIO ( c.g.c)
===> góc HGA = góc IGO (góc tương ứng của 2 t.giác đ.dạng )
Vì góc HGA và góc IGO là 2 góc ở vị trí đối đỉnh bằng nhau nên ta suy ra H , G , O thẳng hàng .
Vậy trong 1 tam giác trực tâm , trọng tâm , tâm đường tròn ngoại tiếp cùng nằm trên 1 đường thẳng đó là đường thẳng Euler !
hok tốt
Đúng 0
Bình luận (0)
1.Cho trước điểm A nằm ngoài đường thẳng a và đường thẳng d vuông góc với đường thẳng a. Bằng phường pháp phản chứng và tiên đề Ơ-clit hãy chứng minh rằng :qua A chỉ có thể vẽ được 1 đường thẳng d' vuông góc với đường thẳng d.
cho trước điểm A nằm ngoài đường thẳng a và đường thẳng d vuông góc với đường thẳng a. Bằng phương pháp phản chứng và tiên đề ơ clit hãy chứng minh rằng : qua điểm A chỉ có thể vẽ được 1 đường thẳng d' vuông góc với đường thẳng d
Cho trước điểm A nằm ngoài đường thẳng a và đường thẳng d vuông góc với đường thẳng a. Bằng phương pháp phản chứng và tiên đề Ơ-clit hãy chứng minh: qua điểm A chỉ có thể vẽ được 1 đường thẳng d' vuông góc với đường thẳng d.
Giúp mình với :v
Bài 3. Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng ơ không cắt đoạn BC. Từ B hạ BE vuông góc với ơ tại E và qua C hạ CF vuông góc với ơ tại F. Chứng minh rằng BE+ CF = EF.
Cho trước điểm A nằm ngoài đường thẳng a và đường thẳng d vuông góc với đường thẳng a. Bằng phương pháp phản chứng và tiên đề Ơ-clit hãy chứng minh rằng: qua điểm A chỉ có thể vẽ được 1 đường thẳng d' vuông góc với đường thẳng d.
giúp mình với >_<
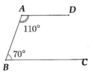
Cho hình vẽ bên.a) Chứng minh AD song song với BC.b) Trên nửa mặt phẳng có bờ là đường thẳng AB không chứa điểm D, lấy điểm E sao cho 70°. Chứng minh E, A, D thẳng hàng theo hai cách sau:Cách 1: Chứng minh 180°.Cách 2: Sử dụng tiên đề Ơ-clit.
Đọc tiếp
Cho hình vẽ bên.
a) Chứng minh AD song song với BC.
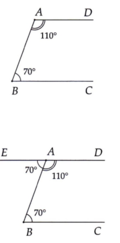
b) Trên nửa mặt phẳng có bờ là đường thẳng AB không chứa điểm D, lấy điểm E sao cho = 70°. Chứng minh E, A, D thẳng hàng theo hai cách sau:
Cách 1: Chứng minh = 180°.
Cách 2: Sử dụng tiên đề Ơ-clit.
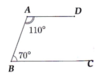
a) Ta có D A B ^ + A B C ^ = 180°.
Mà hai góc ở vị trí trong cùng phía.
Từ đó AD // BC (tính chất hai đường thẳng song song).
b) Cách 1:
E A B ^ + B A D ^ = 70° + 110° = 180°
Cách 2: E A B ^ = A B C ^ = 70°
Mà hai góc ở vị trí so le trong nên AE// BC ( tính chất hai đường thẳng song song)
Lại có AD//BC ( chứng minh ý a)) nên Ad = AE.
Vậy E, A, D thẳng hàng
Đúng 0
Bình luận (0)
Cho hình vẽ bên.a) Chứng minh AD song song với BC.b) Trên nửa mặt phẳng có bờ là đường thẳng AB không chứa điểm D, lấy điểm E sao cho
B
A
E
^
70
°
. Chứng minh E, A,D thẳng hàng theo hai cách sau:Cách 1: Chứng minh
E
A
D
^
180
°
.Cách 2: Sử dụng tiên đề Ơ-clit.
Đọc tiếp
Cho hình vẽ bên.
a) Chứng minh AD song song với BC.
b) Trên nửa mặt phẳng có bờ là đường thẳng AB không chứa điểm D, lấy điểm
E sao cho B A E ^ = 70 ° . Chứng minh E, A,
D thẳng hàng theo hai cách sau:
Cách 1: Chứng minh E A D ^ = 180 ° .
Cách 2: Sử dụng tiên đề Ơ-clit.