Cho 4 điểm A, B, C và D không đồng phẳng. Gọi \(G_{A;}G_B;G_C;G_D\) lần lượt là trọng tâm của các tam giác BCD, CDA, ABD, ABC. Chứng minh \(AG_A;BG_B;CG_C;DG_D\) đồng quy ?

Những câu hỏi liên quan
Trong không gian Oxyz , cho mặt phẳng
P
:
x
+
y
-
z
-
4
0
và điểm
A
2
,
-
1
,
3
.
Gọi D là đường thẳng đi qua A và song song với (P) , biết D có một vectơ chỉ phương là
u
→
a...
Đọc tiếp
Trong không gian Oxyz , cho mặt phẳng P : x + y - z - 4 = 0 và điểm A 2 , - 1 , 3 . Gọi D là đường thẳng đi qua A và song song với (P) , biết D có một vectơ chỉ phương là u → a , b , c , đồng thời D đồng phẳng và không song song với Oz . Tính a c
A. -1/2
B. 1/2
C. 2
D. – 2
Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (MBC) và mp (NDA) là:
A. AD
B. BC
C. AC
D. MN
Đáp án D

M ∈ AD ⇒ M ∈ (NDA)
N ∈ BC N ∈ ( MBC)
Xét (NDA) và (MBC) có
M là điểm chung
N là điểm chung
⇒ Giao tuyến của 2 mặt phẳng là MN
Đúng 0
Bình luận (0)
Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (AMN) và mp (BCD) là:
A. ND
B. BC
C. CD
D. MN
Đáp án A

D ∈ AM ⇒ D ∈ (AMN)
N ∈ BC ⇒ N ∈ (BCD)
Xét (AMN) và (BCD) có:
D là điểm chung
N là điểm chung
⇒ Giao tuyến của 2 mặt phẳng là ND
Đúng 0
Bình luận (0)
Cho 4 điểm A, B, C và D không đồng phẳng. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.
a) Tìm giao điểm của đường thẳng CD và mặt phẳng (MNP)
b) Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD)
a) Gọi \(NP\cap CD=K\).
Do \(K\in NP\) nên \(K\in\left(MNP\right)\). Vậy K là giao điểm của CD và (MNP).
b) Do \(M\in AC\) nên \(M\in\left(MNP\right)\cap\left(ACD\right)\).
Và K là giao điểm của CD và (MNP) nên \(K\in\left(MNP\right)\cap\left(ACD\right)\).
Vì vậy MK là giao tuyến của (MNP) và (ACD).
Đúng 0
Bình luận (0)
Cho 4 điểm A, B, C, D không đồng phẳng. Gọi M, N lần lượt là trung điểm của AB, AD. P là điểm trên đoạn AC sao cho PA=2PC. Tìm giao tuyến của (MP) và (BCD)
Trong mp (ABC), nối MP kéo dài cắt BC kéo dài tại E
Trong mp (ACD), nối NP kéo dài cắt CD kéo dài tại F
\(\Rightarrow EF=\left(MNP\right)\cap\left(BCD\right)\)
Đúng 1
Bình luận (0)
Cho 4 điểm A, B, C và D không đồng phẳng. Gọi I, K lần lượt là trung điểm của hai đoạn thẳng AD và BC
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD)
b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN)
a) Chứng minh I, K là hai điểm chung của (BIC) và (AKD)
b) Gọi P = CI ∩ DN và Q = BI ∩ DM, chứng minh PQ là giao tuyến cần tìm.
Đúng 0
Bình luận (0)
a) \(I\in AD\) nên \(I\in\left(IBC\right)\cap\left(KAD\right)\);
\(K\in BC\) nên \(K\in\left(IBC\right)\cap\left(KAD\right)\).
Vì vậy: \(IK\in\left(IBC\right)\cap\left(KAD\right)\).
b)
Gọi \(P=CI\cap DN\) . Do \(\left\{{}\begin{matrix}P\in CI\\P\in DN\end{matrix}\right.\) nên \(P\in\left(IBC\right)\cap\left(DMN\right)\).
Gọi \(Q=BI\cap MD\). Do \(\left\{{}\begin{matrix}Q\in BI\\Q\in MD\end{matrix}\right.\) nên \(Q\in\left(IBC\right)\cap\left(DMN\right)\).
Vậy PQ là giao tuyến của (IBC) và (DMN).
Đúng 0
Bình luận (0)
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I, K lần lượt là trung điểm của AD và BC.
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD).
b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN).
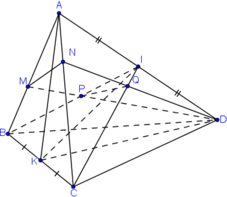
a) Tìm giao tuyến của mp(IBC) và mp(KAD).
Ta có:
K ∈ BC ⇒ K ∈ (IBC) ⇒ K ∈ (IBC) ∩ (KAD)
I ∈ AD ⇒ I ∈ (KAD) ⇒ I ∈ (IBC) ∩ (KAD)
Vậy KI = (IBC) ∩ (KAD)
b) Trong mp(ABD) gọi BI ∩ DM = P
⇒ P ∈ (IBC) ∩ (DMN)
Trong mặt phẳng (ACD) gọi CI ∩ DN = Q
⇒ Q ∈ (IBC) ∩ (DMN)
Vậy (IBC) ∩ (DMN) = PQ.
Đúng 1
Bình luận (0)
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi M và N lần lượt là trung điểm của các đoạn thẳng AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.
a) Tìm giao điểm của đường thẳng CD và mặt phẳng (MNP).
b) Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD).
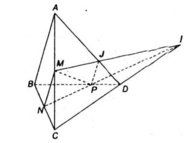
a) Ta có:
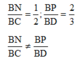
⇒ NP và CD không song song với nhau.
Gọi giao điểm NP và CD là I.
I ∈ NP ⇒ I ∈ (MNP).
Mà I ∈ CD
Vậy I ∈ CD ∩ (MNP)
b) Trong mặt phẳng (ACD) thì AD và MI cắt nhau tại điểm J:
J ∈ AD ⇒ J ∈ (ACD)
J ∈ MI ⇒ J ∈ (MNP)
Vậy J là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Ta đã có M là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Vậy MJ = (ACD) ∩ (MNP).
Đúng 0
Bình luận (0)
Cho hai gương phẳng G, và G_{2} vuông góc với nhau. Đặt một điểm súng S và một điểm M trước gương sao cho SM song song với gương G
. a) Hãy vẽ 1 tia sáng từ 8 tới gương G_{1} sao cho sau khi phản xạ trên
gương G_{2} sẽ lại đi qua M.
b) Cho SM a khoảng cách từ S đến G_{1} là b, khoảng cách từ 5 đền G_{2} là c, vận tốc truyền ánh sáng là v. Hãy tính thời gian truyền của tia sáng từ S đến M theo con đường vẽ được của câu a
Đọc tiếp
Cho hai gương phẳng G, và G_{2} vuông góc với nhau. Đặt một điểm súng S và một điểm M trước gương sao cho SM song song với gương G . a) Hãy vẽ 1 tia sáng từ 8 tới gương G_{1} sao cho sau khi phản xạ trên gương G_{2} sẽ lại đi qua M. b) Cho SM = a khoảng cách từ S đến G_{1} là b, khoảng cách từ 5 đền G_{2} là c, vận tốc truyền ánh sáng là v. Hãy tính thời gian truyền của tia sáng từ S đến M theo con đường vẽ được của câu a










