Cách tính cấp 2 khó hiểu quá, Cứ a b c d khó hiểu quá . MN bày mih cho mình đẽ hỉu hơn đê

Những câu hỏi liên quan
Mn giúp em bài 11c và bài 4f với ạ mai em nộp rồi
Riêng bài 4f thì em có tìm được 1 dạng giải nhưng khó hiểu quá, ai có cách nào dễ hiểu hơn thì giúp em với

11c.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}\dfrac{16a-b^2}{4a}=\dfrac{9}{2}\\16a+4b+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b^2=-4a\\b=-4a-1\end{matrix}\right.\)
\(\Rightarrow2b^2-b=1\Leftrightarrow2b^2-b-1=0\Rightarrow\left[{}\begin{matrix}b=1\Rightarrow a=-\dfrac{1}{2}\\b=-\dfrac{1}{2}\Rightarrow a=-\dfrac{1}{8}\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=-\dfrac{1}{2}x^2+x+4\\y=-\dfrac{1}{8}x^2-\dfrac{1}{2}x+4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
4f.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}1+b+c=0\\\dfrac{4c-b^2}{4}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-b-1\\c=\dfrac{b^2}{4}-1\end{matrix}\right.\)
\(\Rightarrow\dfrac{b^2}{4}+b=0\)
\(\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow c=-1\\b=-4\Rightarrow c=3\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=x^2-1\\y=x^2-4x+3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
mn giúp em vs ạ. bài này em khó hiểu quá ạ
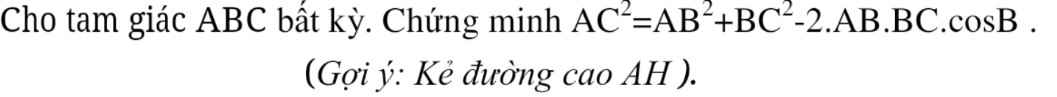
Kẻ AH⊥BC
ta có: \(VP=AB^2+BC^2-2.AB.BC.cosB=AB^2+BC^2-2.AB.BC.\dfrac{BH}{AB}=AB^2+BC^2-2.BH.BC=AB^2-BH^2+BC^2-2.BH.BC+BH^2=AH^2+\left(BC-BH\right)^2=AH^2+CH^2=AC^2=VT\)
Đúng 1
Bình luận (0)
Cho tỉ lệ thức a/b c/d.Chứng minh rằng: ac/bd a2 + c2/b2+d2.Ở đây mình không biết ghi kiểu phân số nên nhìn hơi rối. Nếu không hiểu các bạn có thể xem ở SBT toán 7 tập 1 trang 21 bài 7.4*. Mở sách ra thì có phần đáp án nhưng mình nhìn thì thấy nó khó hiểu quá nên mình cần một bài giải ngắn gọn hơn và dễ hiểu hơn.Thanks trước ạ!!P/S: Tiện thể cho mình hỏi cách đánh phân số trong Online Math như thế nào và đổi tên trong Online Math ở đâu. Yêu nhiều mọi người!!!
Đọc tiếp
Cho tỉ lệ thức a/b = c/d.
Chứng minh rằng: ac/bd = a2 + c2/b2+d2.
Ở đây mình không biết ghi kiểu phân số nên nhìn hơi rối. Nếu không hiểu các bạn có thể xem ở SBT toán 7 tập 1 trang 21 bài 7.4*. Mở sách ra thì có phần đáp án nhưng mình nhìn thì thấy nó khó hiểu quá nên mình cần một bài giải ngắn gọn hơn và dễ hiểu hơn.
Thanks trước ạ!!
P/S: Tiện thể cho mình hỏi cách đánh phân số trong Online Math như thế nào và đổi tên trong Online Math ở đâu. Yêu nhiều mọi người!!!
Đặt \(\frac{a}{b}=\frac{c}{d}=k\) thì a = bk ; c = dk
Ta có : \(\frac{ab}{cd}=\frac{bk.dk}{bd}=\frac{bd.k^2}{bd}=k^2\) (1)
\(\frac{a^2+c^2}{b^2+d^2}=\frac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\frac{b^2k^2+d^2k^2}{b^2+d^2}=\frac{\left(b^2+d^2\right).k^2}{b^2+d^2}=k^2\) (2)
Từ (1) và (2) suy ra \(\frac{ac}{bd}=\frac{a^2+c^2}{b^2+d^2}\)
Đúng 0
Bình luận (0)
Giải bài này hộ mình với khó hiểu quá 
x ∈ {năng lượng gió, năng lượng mặt trời, năng lượng địa nhiệt}
y ∈ {năng lượng gió, năng lượng mặt trời}
Đúng 1
Bình luận (0)
Giúp em với mn ơi mai e phải nôp bài rồi mà khó hiểu quá mong mn giúp e 
a) \(n_{Zn}=\dfrac{13}{65}=0,2\left(mol\right);n_{H_2SO_4}=0,1.2,5=0,25\left(mol\right)\)
PTHH: Zn + H2SO4 → ZnSO4 + H2
Mol: 0,2 0,2 0,2 0,2
Ta có: \(\dfrac{0,2}{1}< \dfrac{0,25}{1}\) ⇒ Zn hết, H2SO4 dư
b) \(V_{H_2}=0,2.22,4=4,48\left(l\right)\)
c) \(m_{ZnSO_4}=0,2.161=32,2\left(g\right)\)
\(m_{H_2SO_4\left(dư\right)}=\left(0,25-0,2\right).98=4,9\left(g\right)\)
Đúng 3
Bình luận (1)
Bài 2 :
\(n_{Zn}=\dfrac{13}{65}=0,2\left(mol\right)\)
100ml = 0,1l
\(n_{H2SO4}=2,5.0,1=0,25\left(mol\right)\)
a) Pt : \(Zn+2H_2SO_4\rightarrow ZnSO_4+H_2|\)
1 1 1 1
0,2 0,25 0,2 0,2
b) Lập tỉ số so sánh : \(\dfrac{0,2}{1}< \dfrac{0,25}{2}\)
⇒ Zn phản ứng hết , H2SO4 dư
⇒ Tính toán dựa vào số mol của Zn
\(n_{H2}=\dfrac{0,2.1}{1}=0,2\left(mol\right)\)
\(V_{H2\left(dktc\right)}=0,2.22,4=4,48\left(l\right)\)
c) \(n_{ZnCl2}=\dfrac{0,2.1}{1}=0,2\left(mol\right)\)
⇒ \(m_{ZnCl2}=0,2.136=27,2\left(g\right)\)
\(n_{H2SO4\left(dư\right)}=0,25-0,2=0,05\left(mol\right)\)
⇒ \(m_{H2SO4\left(dư\right)}=0,05.98=4,9\left(g\right)\)
Chúc bạn học tốt
Đúng 1
Bình luận (1)
Ta có: \(n_{Zn}=\dfrac{13}{65}=0,2\left(mol\right)\)
a. PTHH: Zn + H2SO4 ---> ZnSO4 + H2
b. Đổi 100ml = 0,1 lít
Ta có: \(C_{M_{H_2SO_4}}=\dfrac{n_{H_2SO_4}}{0,1}=2,5M\)
=> \(n_{H_2SO_4}=0,25\left(mol\right)\)
Ta thấy: \(\dfrac{0,2}{1}< \dfrac{0,25}{1}\)
=> H2SO4 dư
Theo PT: \(n_{H_2}=n_{Zn}=0,2\left(mol\right)\)
=> \(V_{H_2}=0,2.22,4=4,48\left(lít\right)\)
c. Theo PT: \(n_{ZnSO_4}=n_{Zn}=0,2\left(mol\right)\)
=> \(m_{ZnSO_4}=0,2.161=32,2\left(g\right)\)
Ta có: \(m_{H_2}=0,2.2=0,4\left(g\right)\)
\(m_{H_2SO_4}=0,25.98=24,5\left(g\right)\)
Ta có:
- Khối lượng ở vế trái là: 24,5 + 13 = 37,5(g)
- Khối lượng vế phải là: 0,4 + 32,2 = 32,6(g)
=> Khối lượng chất còn lại sau phản ứng là:
37,5 - 32,6 = 4,9(g)
Đúng 1
Bình luận (1)
giải thích cách chứng minh bổ đề Bezout giùm mình
thầy giảng khó hiểu quá! nhớ giải thích tường tận nha
sách nâng cao và phát toán 8 tập 1 giở mà coi
Đúng 0
Bình luận (0)
Cho a,b,c>0 và a+b+c\(\le\dfrac{3}{2}\).Tìm GTNN của biểu thức
\(Q=\sqrt{a^2+\dfrac{1}{b^2}}+\sqrt{b^2+\dfrac{1}{c^2}}+\sqrt{c^2+\dfrac{1}{a^2}}\)
Đừng trình bày quá vắn tắt (khó hỉu =[[) đừng dùng các bất đẳng thức quốc tế như bunhiacopxki,svácxơ,....
\(không\) \(dùng\) \(bđt\) \(làm\) \(sao\) \(ra\) \(được\) ??
\(\sqrt{a^2+\dfrac{1}{b^2}}=\dfrac{1}{\sqrt{17}}.\sqrt{\left(1+4^2\right)\left(a^2+\dfrac{1}{b^2}\right)}\ge\dfrac{1}{\sqrt{17}}\left(a+\dfrac{4}{b}\right)\left(bunhiacopki\right)\)
\(tương-tự:\sqrt{b^2+\dfrac{1}{c^2}}\ge\dfrac{1}{\sqrt{17}}\left(b+\dfrac{4}{c}\right)\)
\(\sqrt{c^2+\dfrac{1}{a^2}}\ge\dfrac{1}{\sqrt{17}}\left(c+\dfrac{4}{a}\right)\)
\(\Rightarrow Q\ge\dfrac{1}{\sqrt{17}}\left(a+b+c+\dfrac{4}{a}+\dfrac{4}{b}+\dfrac{4}{c}\right)=\dfrac{1}{\sqrt{17}}\left[16a+\dfrac{4}{a}+16b+\dfrac{4}{b}+16c+\dfrac{4}{c}-15\left(a+b+c\right)\right]\)
\(bđt:cosi\Rightarrow16a+\dfrac{4}{a}\ge2\sqrt{16a.\dfrac{4}{a}}=2\sqrt{16.4}=16\)
\(tương-tự\Rightarrow16b+\dfrac{4}{b}\ge16;16c+\dfrac{4}{c}\ge16\)
\(có:a+b+c\le\dfrac{3}{2}\Rightarrow15\left(a+b+c\right)\le\dfrac{45}{2}\)
\(\Rightarrow-15\left(a+b+c\right)\ge-\dfrac{45}{2}\)
\(\Rightarrow Q\ge\dfrac{1}{\sqrt{17}}\left(16+16+16-\dfrac{45}{2}\right)=\dfrac{3\sqrt{17}}{2}\)
\(dấu"="xayra\Leftrightarrow a=b=c=\dfrac{1}{2}\)
các bước ban đầu dùng bunhia chọn được 1+4^2 là do dự đoán được trước điểm rơi tại a=b=c=1/2 thôi bạn,cả bước tách dùng cosi cũng dự đoán dc điểm rơi =1/2 nên tách đc thôi
Đúng 0
Bình luận (0)
Tại sao lại k được dùng nhỉ? Trông khi dùng thì bài toán sẽ dễ giải quyết hơn
Áp dụng Bunhiacopxki:
\(\sqrt{\left(a^2+\dfrac{1}{b^2}\right)\left(\dfrac{1}{4}+4\right)}\ge\dfrac{a}{2}+\dfrac{2}{b}\)
\(\Rightarrow\sqrt{a^2+\dfrac{1}{b^2}}\ge\dfrac{2}{\sqrt{17}}\left(\dfrac{a}{2}+\dfrac{2}{b}\right)\)
Do đó:
\(Q\ge\dfrac{2}{\sqrt{17}}\left[\dfrac{a+b+c}{2}+2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\right]\)
Ta có: \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{9}{a+b+c}\)
\(\Rightarrow Q\ge\dfrac{2}{\sqrt{17}}\left[\dfrac{a+b+c}{2}+\dfrac{18}{a+b+c}\right]\)
Áp dụng Cô-si:
\(\dfrac{a+b+c}{2}+\dfrac{9}{8\left(a+b+c\right)}\ge\dfrac{3}{2}\)
Do đó:
\(Q\ge\dfrac{2}{\sqrt{17}}\left[\dfrac{3}{2}+\dfrac{135}{8\left(a+b+c\right)}\right]\ge\dfrac{2}{\sqrt{17}}\left[\dfrac{3}{2}+\dfrac{135}{8.\dfrac{3}{2}}\right]=\dfrac{3\sqrt{17}}{2}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{2}\)
Đúng 0
Bình luận (2)
Cách này 100% dùng Cô-si
Áp dụng Cô-si:
\(Q\ge3\sqrt[3]{\sqrt{\left(a^2+\dfrac{1}{b^2}\right)\left(b^2+\dfrac{1}{c^2}\right)\left(c^2+\dfrac{1}{a^2}\right)}}\)
Ta có:
\(A=\left(a^2+\dfrac{1}{b^2}\right)\left(b^2+\dfrac{1}{c^2}\right)\left(c^2+\dfrac{1}{a^2}\right)\)
\(=\left(a^2+b^2+c^2\right)+\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)+\left(abc\right)^2+\dfrac{1}{\left(abc\right)^2}\)
Áp dụng Cô-si:
\(a^2+\dfrac{1}{16a^2}\ge\dfrac{1}{2}\)
Tương tự với các phần còn lại
\(\Rightarrow A\ge\dfrac{3}{2}+\dfrac{15}{16}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)+\left(abc\right)^2+\dfrac{1}{\left(abc\right)^2}\)
Ta có:
\(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge3\sqrt[3]{\dfrac{1}{\left(abc\right)^2}}\ge3\sqrt[3]{\dfrac{1}{\left[\dfrac{\left(a+b+c\right)^3}{27}\right]^2}}\ge12\) (Cô-si)
\(\left(abc\right)^2+\dfrac{1}{64^2\left(abc\right)^2}\ge\dfrac{1}{32}\) (Cô-si)
\(\Rightarrow A\ge\dfrac{3}{2}+\dfrac{15}{16}.12+\dfrac{1}{32}+\dfrac{4095}{64^2\left(abc\right)^2}\)
Mà:
\(abc\le\dfrac{\left(a+b+c\right)^3}{27}=\dfrac{1}{8}\)
\(\Rightarrow A\ge\dfrac{3}{2}+\dfrac{15}{16}.12+\dfrac{1}{32}+\dfrac{4095}{64^2.\dfrac{1}{8^2}}=\dfrac{4913}{64}\)
\(\Rightarrow Q\ge3\sqrt[3]{\sqrt{A}}\ge\dfrac{3\sqrt{17}}{2}\)
Đúng 0
Bình luận (1)
Một ô tô đi từ tỉnh a qua tỉnh b dến tinh c hết 5 giờ .Thời gian đi từ a đền b bằng 2/3 thời gian đi từ bđền c .Vận tốc đi từ a đến b hơn vận tôc đi từ b đến c là 8 km/giờ .Quãng đường bc là 30 km .tính quãng dường ac [ tớ hiểu bài này rồi nhưng trinh bày khó quá giup tớ nhé!!!!!!]
Dân ta phải biết sử ta
Bài nào không biết thì tra google
Đúng 0
Bình luận (0)
Các bn giúp mik làm nhé,khó hiểu quá mik ko làm được:
cho tam giác ABC biết góc C=43 độ;góc B=82 độ .Tính số đo góc A
ap dung t/c tong 3 goc =180 do
=>goc A+gocB+gocC =180 do
thay: B=82 do
C=43 do
ta duoc A+82+43=180
A+125=180
A =180 -125
A =55 do
co len nha ban
\(\text{Xét }\Delta ABC\text{ có:}\)
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\text{(tính chất tổng 3 góc của 1 tam giác)}\)
\(\Rightarrow\widehat{A}=180^0-\left(\widehat{B}+\widehat{C}\right)\)
\(\Rightarrow\widehat{A}=180^0-\left(82^0+43^0\right)=55^0\)
Đúng 0
Bình luận (0)




























