cho tam giác ABC , hai tia phân giác của góc b và góc c cắt tại I . cmr góc BIC = 90 độ + góc A/2

Những câu hỏi liên quan
cho tam giác abc có góc A bằng 60 độ các tia phân giác trong của góc B và C cắt tại I , các tia phân giác ngoài của góc B và C cắt nhau tại K . tia BI cắt KC tại D. Tính góc BIC , góc BKC , CMR góc BDC= BAC /2
Cho tam giác ABC, các đường phân giác của góc B và góc C cắt nhau tại I.
a,Nếu góc BIC = 140 độ, hãy tính số đo góc BAC.
b,CMR: góc BTC=90 độ + góc DAC/2.
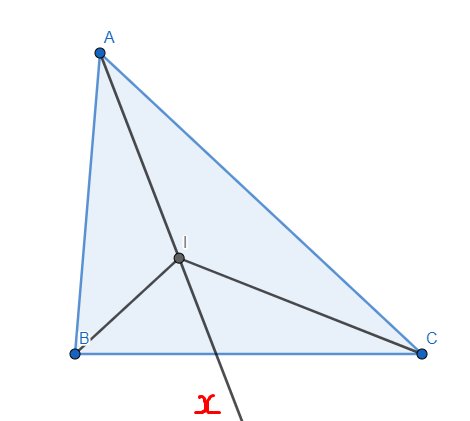
Kẻ tia phân giác Ax của tam giác ABC. Theo tính chất góc ngoài của tam giác, dễ có \(\widehat{BIx}=\widehat{IBA}+\widehat{IAB}\) và \(\widehat{CIx}=\widehat{ICA}+\widehat{IAC}\). Cộng theo vế 2 đẳng thức trên, thu được \(\widehat{BIC}=\dfrac{\widehat{ABC}}{2}+\dfrac{\widehat{ACB}}{2}+\widehat{ABC}\) \(=\dfrac{180^o+\widehat{ABC}}{2}\) \(=90^o+\dfrac{\widehat{BAC}}{2}\)
Tới đây mình cũng đã chứng minh xong câu b luôn rồi. Bạn chỉ cần thay số đo góc vào thì tính được câu a.
Đúng 1
Bình luận (0)

a) (BI và CI lần lượt là các đường phân giác của góc B và C)
Theo đề ta có:
\(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^o\)
\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=180^o-\widehat{BIC}=180^o-140^o=40^o\)
Mà \(\widehat{ABI}=\widehat{CBI}\) và \(\widehat{ACI}=\widehat{BCI}\) (vì BI và CI lần lượt là các đường phân giác của góc B và C)
Suy ra \(\widehat{ABC}+\widehat{ACB}=2\widehat{IBC}+2\widehat{ICB}=2\left(\widehat{IBC}+\widehat{ICB}\right)=2\cdot40^o=80^o\)
Từ đó
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\)
\(\Leftrightarrow\widehat{BAC}=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)=180^o-80^o=100^o\)
Đúng 1
Bình luận (0)
cho tam giác ABC có AB<AC, tia phân giác góc B cắt tia phân giác góc C tại I c/m góc BIC = 90 độ + 1/2 góc A
cho tam giác ABC có AB<AC, tia phân giác góc B cắt tia phân giác góc C tại I c/m góc BIC = 90 độ + 1/2 góc A
cho tam giác ABC có 2 góc ngoài là góc CBx và góc BCy.Hai tia phân giác của 2 góc ngoài này cắt nhau tại I.
a, CM góc IBC = 90 độ - 1/2 góc B và góc ICB=90 độ - 1/2 góc C
b, CM góc BIC =1/2(góc ABC + góc ACB)
c, Cho góc A = 60 độ .Tính góc BIC
Cho tam giác ABC . Các tia phân giác của góc B và góc C cắt nhau tại I . CMR : Góc BIC = góc A
1.Cho tam giác ABC có A + B = C + 90 và A = C + 10. Tính các góc của tam giác ABC
2.Cho tam giác ABC vuông tại A, vẽ các tia phân giác của B và C cắt nhau tại M. Tính BMC
3.Cho tam giác ABC có A =80, B = 60. Hai tia phân giác của B và c cắt nhau tại I, vẽ tia p/g góc ngoài tại B sao cho B cắt tia CI tại D
a) Tính BIC
b)CMR BDC = C
1, Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(tổng 3 góc tam giác)
\(\Leftrightarrow\widehat{C}+90^o+\widehat{C}=180^o\)
\(\Leftrightarrow2\widehat{C}=90^o\)
\(\Leftrightarrow\widehat{C}=45^o\)
\(\Rightarrow\widehat{A}=\widehat{C}+10=55^o\)
\(\Rightarrow\widehat{B}=180^o-\widehat{A}-\widehat{C}=180^o-55^o-45^o=80^o\)
Đúng 0
Bình luận (0)
2,
Vì tam giác ABC vuông tại A
=> ^B + ^C = 90o
Vì BM là phân giác ^ABC
=>^B1 = \(\frac{\widehat{ABC}}{2}\)
Tương tự ^C1 = \(\frac{\widehat{ACB}}{2}\)
\(\Rightarrow\widehat{B_1}+\widehat{C_1}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{90^o}{2}=45^o\)
Theo tổng 3 góc trong tam giác \(\widehat{BMC}=180^o-\widehat{B_1}-\widehat{C_1}=180^o-45^o=135^o\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A=90 độ.Tia phân giác của góc B cắt tia phân giác của góc C tại I. Tính góc BIC
vì góc A bằng 90 độ nên:
góc B + góc C = 180-90=90 độ
\(\Rightarrow\)góc BIC = 180 - (90 : 2) = 135 độ
Đúng 1
Bình luận (0)
cho tam giác ABC ,2 đưiơng phân giác trong của các góc B vá C cắt nhau tại I, phân giác ngoài của 2 góc B và C cắt nhau tại J. Đường phân giác trong của góc B và đương phân giác ngoài của góc C cắt nhau tại K. Tính góc BIC theo góc A của tam giác ABC
(CHỈ CẦN TÍNH :BIC +90-A/2=180 LÀ RA ĐƯỢC GÓC BIC)
















