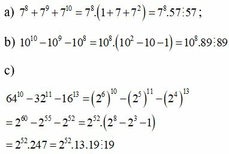a,  7 8 + 7 9 + 7 10 = 7 8 . 1 + 7 + 7 2 =  7 8 . 57 ⋮ 57

b,  10 10 - 10 9 - 10 8 =  10 8 . ( 10 2 - 10 - 1 ) =  10 8 . 89 ⋮ 89

c,  64 10 - 32 11 - 16 3 = ( 2 6 ) 10 - ( 2 ⁵ ) 11 - ( 2 4 ) 13 =  2 60 - 2 55 - 2 52 = 2 52 2 8 - 2 3 - 1

=  2 52 . 247 = 2 52 . 13 . 19 ⋮ 19

a) Ta có: \(10^{10}=10...0\) nên \(10^{10}-1=10...0-1=99...9\)

Nên: \(10^{10}-1⋮9\)

b) Ta có: \(10^{10}=10...0\) nên: \(10^{10}+2=10...0+2=10...2\)

Mà: \(1+0+...+2=3\)

Nên: \(10^{10}+2⋮3\)

c) Gọi số chẵn đó \(a\) số chẵn tiếp theo là:\(a+2\)

Mà tổng của 2 số chẵn đó là:

\(a+a+2=2a+2=2\left(a+1\right)\) không chia hết cho 4 nên 

Tổng của 2 số chẵn liên tiêp ko chia hết cho 4

d) Gọi hai số tự nhiên đó là: \(a,a+1\)

Tích của 2 số tự nhiên đó là:

\(a\left(a+1\right)=a^2+a\) 

Nếu a là số lẻ thì \(a^2\) lẻ nên \(a^2+a\) là chẳn

Nếu a là số chẵn thì \(a^2\) chẵn nên \(a^2+a\) là chẵn 

Vậy tích của hai số liên tiếp là chẵn

e) Gọi hai số đó là: \(2a,2a+2\)

Tích của hai số đó là:

\(2a\cdot\left(2a+2\right)=4a^2+4a=4a\left(a+1\right)\) 

4a(a+1) chia hết cho 8 nên

Tích của hai số tự nhiên liên tiếp chia hết cho 8

d) Gọi một số tự nhiên bất kỳ là a 

\(\Rightarrow\) Số tự nhiên liền kề là a+1

Nếu a là số lẻ thì a+1 là số chẵn

\(\Rightarrow a\left(a+1\right)\) là số chẵn

Nếu a là số chẵn thì \(a\left(a+1\right)\) là số chẵn 

Vậy tích hai số TN liên tiếp bao giờ cũng là một số chẵn

e) Gọi hai số chẵn liên tiếp lần lượt là 2a và 2a+2 ( a là một số TN bất kỳ )

Ta có \(2a\left(2a+2\right)=2a.2\left(a+1\right)=4a\left(a+1\right)\)

Ta chứng minh được tích hai số TN liên tiếp bao giờ cũng là một số chẵn

\(\Rightarrow a\left(a+1\right)\) có dạng 2k ( k bất kỳ )

\(\Rightarrow2a\left(2a+2\right)=8k⋮8\) 

Vậy tích hai số chẵn liên tiếp chia hết cho 8

ta có :   n+18 và n+19 là hai số tự nhiên liên tiếp 

nên tích của chúng là một số chẵn

 mà một số chẵn luôn chia hết cho hai 

  vậy nó chia hết cho 2

ai trả lời nhanh thì tôi k cho nhiều nhất

Vậ

Ta có:37⁴⁹=37.(37⁴)¹²=37.\(\left(\overline{...1}^{12}\right)\)=37.\(\left(\overline{...1}\right)\)=\(\left(\overline{...7}\right)\)

=>Chữ số tận cùng của 37⁴⁹ là 7

Mà \(\left(\overline{...7}\right)\)+108=\(\left(\overline{...5}\right)\)\(⋮\)5

Vậy 37⁴⁹+108\(⋮\)5

Đánh nhầm,bỏ dòng đầu tiên đi nhé

Mình đùa chút nhé:

Cần j chứng minh, thấy nó đúng là đc mà!

mình nghĩ c/m là cái điều đấy nó đã đúng sẵn rồi

nên chắc chẳng cần c/m đâu nhỉ =)

mình ko hiểu lắm các bạn giúp mình

Có : 108 = 9x6x2

và    12 = 6 x 2

=> 108 chia hết cho 12

có:108:12=9*2*6

vì:12=2*6

=>108:hết cho 12

*Một số tn bất kỳ khi chia cho 2015 có số dư là 1 trong 2014 số :.....

*Sau đó ta chia 1010 thành 1009 nhóm

*Theo nguyên lý Dirichlet ta có 2 trường hợp

Ta có ĐPCM

Giả sử 6 số đó tồn tại 1 cặp có cùng tận cùng (Ví dụ 1236, 26), vậy hiệu chia hết cho 5. Thỏa mãn

Giả sử không có cặp số nào cùng tận cùng, vậy các chữ số tận cùng có thể là: 1, 2, 3, 4, 6, 7, 8, 9

Các cặp có hiệu chia hết cho 5 là: 6 - 1, 7 - 2, 8 -3, 9 - 4, nếu bỏ đi 2 số bất kỳ vẫn tồn tại 2 cặp có hiệu chia hết cho 5. CM xong!