Bạn giỏi thật, lớp 8 mà đã đi giải toán lớp 9

ừ mik muốn tìm hiểu 

ồ bạn giống mk lớp 8 đg ôn thi toán lướp 9 tỉnh nek violympic :D

Giải:

Gọi \(x\) là số sản phẩm loại I mà xí nghiệp sản xuất được trong \(1\) giờ \(\left(x>0\right)\)

\(\Rightarrow\) Số sản phẩm loại II sản xuất được trong một giờ là \(x+10\)

Thời gian sản xuất \(120\) sản phẩm loại I là \(\dfrac{120}{x}\) (giờ)

Thời gian sản xuất \(120\) sản phẩm loại II là \(\dfrac{120}{x+10}\) (giờ)

Theo bài ra ta có phương trình: \(\dfrac{120}{x}+\dfrac{120}{x+10}=7\left(1\right)\)

Giải phương trình \(\left(1\right)\) ta được: \(\left\{{}\begin{matrix}x_1=30\left(\text{chọn}\right)\\x_2=\dfrac{-40}{7}\left(\text{loại}\right)\end{matrix}\right.\)

Vậy mỗi giờ xí nghiệp sản xuất được \(30\) sản phẩm loại I và \(40\) sản phẩm loại II

Chọn B

Vậy để thu được lợi nhuận cao nhất thì cần sản xuất 20 sản phẩm loại I và 40 sản phẩm loại II

Chọn C

+ Gọi x( x ≥ 0 )  là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.

Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y

Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra

2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0

+ Tìm x; y thoả mãn hệ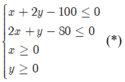 

sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.

Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0

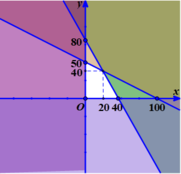
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ

Giá trị lớn nhất của L( x; y)  đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)

+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;

L(0; 50) = 1.500.000; L(20; 40) =  2.000.000

suy ra giá trị lớn nhất của L(x; y)  là 2.000.000 khi (x; y) =(20; 40).

Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.

+ Gọi x( x ≥ 0 )  là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.

Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y

Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra

2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0

+ Tìm x; y thoả mãn hệ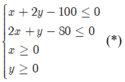 

sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.

Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0

Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ

Giá trị lớn nhất của L( x; y)  đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)

+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;

L(0; 50) = 1.500.000; L(20; 40) =  2.000.000

suy ra giá trị lớn nhất của L(x; y)  là 2.000.000 khi (x; y) =(20; 40).

Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.

Gọi số ngày dự định làm theo kế hoạch là x ngày (x > 2)

Số ngày thực tế làm là x – 2 (ngày)

Số sản phẩm sản xuất theo dự định 120.x (sản phẩm), số sản phẩm sản suất theo thực tế 130(x – 2)(sản phẩm)

Theo bài ra ta có phương trình:

120x = 130.(x – 2)

⇔ 120x = 130x – 260

⇔ 10x = 260

⇔ x = 26 (tmđk)

Vậy số sản phẩm xí nghiệp đã sản xuất được là 120.26 = 3120 sản phẩm.