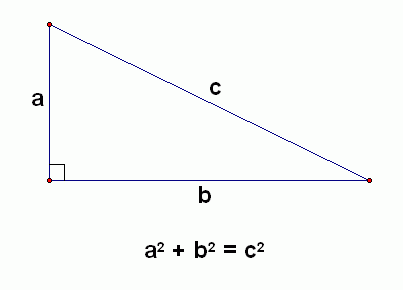
Cho a ; b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của một tam giác vuông. Trong đó c − b ≠ 1  và c + b ≠ 1 . Kết luận nào sau đây là đúng ?

A.  log c + b a + log c − b a = 2 log c + b a log c − b a

B.  log c + b a + log c − b a = log c + b a log c − b a

C.  log c + b a + log c − b a = − 2 log c + b a log c − b a

D.  log c + b a + log c − b a = − log c + b a log c − b a

Cho a; b; c  lần lượt là độ dài của hai cạnh góc vuông và cạnh huyền của một tam giác vuông, trong đó c - b và c + b khác 1. Khi đó log_c+ba + log_c-ba  bằng:

A.-2log_c+ba.log_c-ba.

B. 3log_c+ba.log_c-ba.

C.2log_c+ba.log_c-ba.

D. Tất cả sai

Lấy giấy trắng cắt tám tam giác vuông bằng nhau. Trong mỗi tam giác vuông đó, ta gọi độ dài các cạnh góc vuông là a và b, gọi độ dài cạnh huyền là c. Cắt hai tấm bìa hình vuông có cạnh bằng a+b

Đặt bốn tam giác vuông còn lại lên tấm bìa hình vuông thứ hai như hình 122. Phần bìa không bị che lấp gồm hai hình vuông có cạnh là a và b; tính diện tích phần bìa đó theo a và b

Gọi c là cạnh huyền, a và b là hai cạnh góc vuông của một tam giác vuông. Mệnh đề nào dưới đây đúng 

A.  log b + c a + log c - b a = log b + c a . log c - b a

B.  log b + c a + log c - b a = 3 log b + c a . log c - b a

C.  log b + c a + log c - b a = 1 2 log b + c a . log c - b a

D.  log b + c a + log c - b a = 2 log b + c a . log c - b a

Cho tam giác vuông ABC có a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền, trong đó c − b ≠ 1   v à   c + b ≠ 1 . Hệ thức nào sau đây là đúng?

A.  log c + b a + log c − b a = 2 log c 2 − b 2 a .

B.  log c + b a + log c − b a = log c 2 − b 2 a .

C.  log c + b a + log c − b a = 2 log c + b a . log c − b a

D.  log c + b a + log c − b a = log c + b a . log c − b a

a)Ta xét trong tam giác ABH có $\hat{H}$=$90^o$
=>$\widehat{BAH}$+$\widehat{ABH}$=$90^o$
mà $\widehat{BAH}$+$\widehat{HAC}$=$90^o$=$\hat{A}$(gt)
=>$\widehat{ABH}$=$\widehat{HAC}$.
Xét tam giác BHA và Tam giác AIC có:
AB=AC(gt)
$\hat{H}$=$\widehat{AIC}$=$90^o$(gt)
$\widehat{ABH}$=$\widehat{HAC}$(c/m trên)
=>Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn)
=>BH=AI(hai cạnh tương ứng)
b)Vì Tam giác BHA=Tam giác AIC(c/m trên)
=>IC=AH(hai cạnh tương ứng)
Xét trong tam giác vuông ABH có:
$BH^2$+$AH^2$=$AB^2$
mà IC=AH
=>$BH^2$+$IC^2$=$AB^2$(th này là D nằm giữa B và M)
Ta có thể c/m tiếp rằng D nằm giữa M và C thì ta vẫn c/m được Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn) và $BH^2$+$IC^2$=$AC^2$=$AB^2$
=>$BH^{2} + CI^{2}$ có giá trị ko đổi
c)Ta xét trong tam giác DAC có IC,AM là 2 đường cao và cắt nhau tại N(AM cũng là đường cao do là trung tuyến của tam giác cân xuất phát từ đỉnh và cũng chính là đường cao của đỉnh đó xuống cạnh đáy=>AM vuông góc với DC)
=>DN chính là đường cao còn lại=>DN vuông góc với AC(là cạnh đối diện đỉnh đó)
d)Ta dễ dàng tính được Tam giác DMN cân tại M=>DM=MN(dựa vào số đo của các góc và 1 số c/m trên)
Từ M kẻ đường thẳng ME vuông góc với AD còn MF vuông góc với IC,Ta dễ dàng c/m được tam giác MED=Tam giác MFN(cạnh huyền-góc nhọn)
=>ME=MF(là hai đường vuông góc tại điểm M gióng xuống hai cạnh của góc $\widehat{HIC}$)
Theo tính chất của đường phân giác(Điểm nằm trên đường phân giác của góc này thì cách đều hai cạnh tạo thành góc đó)=>IM là tia phân giác của $\widehat{HIC}$.