Cho ngũ giác ABCDE nội tiếp (O). Biết khoảng cách từ E đến AB; BC;CD lần lượt là \(\dfrac{\sqrt{3}}{2};2\sqrt{2};\sqrt{6}\). Tính khoảng cách từ E đến AD.

Những câu hỏi liên quan
Cho ngũ giác ABCDE nội tiếp đường tròn tâm O. Gọi a,b,c lần lượt là khỏang cách từ E đến đường thẳng AB, BC, CD. Tíh khỏang cách từ E đến AD theo a,b,c.
Cho ngũ giác đều ABCDE nội tiếp đường tròn (O). Tính số đo cung AB
A. 72 °
B. 60 °
C. 120 °
D. 90 °
Chọn đáp án A.
Do ABCDE là ngũ giác đều nội tiếp đường tròn (O) nên:
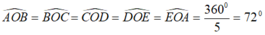
Suy ra, sđ A B ⏜ = 72 °
Đúng 0
Bình luận (0)
Cho đường tròn (O) nội tiếp tam giác ABC với các tiếp điểm là D; E; F lần lượt thuộc các cạnh BC; CA; AB. Chứng minh rằng tích các khoảng cách hạ từ một điểm P bất kì thuộc đường tròn (O) đến các cạnh của tam giác ABC bằng tích các khoảng cách từ điểm P đến các cạnh của tam giác DEF
cho tam giác ABC cân tại A nội tiếp đường tròn tâm O bán kính R biết AB=10 cm BC=12cm tính R và khoảng cách từ O đến các cạnh của tam giác ABC
cho tam giác ABC cân tại A nội tiếp đường tròn tâm O bán kính R biết AB=10 cm BC=12cm tính R và khoảng cách từ O đến các cạnh của tam giác ABC
Cho ngũ giác đều ABCDE nội tiếp đường tròn tâm O bán kính R. Tính \(\left|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}\right|\).
cho đường tròn (o) và đường tròn (o') cắt nhau ở A và B sao cho oo' cắt AB. Đường (d) tiếp xúc o tại C, o' tại D sao cho khoảng cách từ A đến d lớn hơn khoảng cách từ B đến d. Đường thẳng qua A ss đường d cắt (o) tại E và (o') tại F. EC cắt FD tại G, EF cắt CB, DB tại H,K.
a) chung minh tứ giác BCGD nội tiếp
b) tam giac GHK cân
Cho tam giác ABC nội tiếp đường tròn,độ dài 3 cạnh AB,AC,BC lần lượt là 5,12,13.
Khoảng cách từ O đến dây AB là
Cho tam giác abc, đường tròn nội tiếp tâm o. Góc a bằng 45 độ. Góc b bằng 60 độ. Tính khoảng cách từ o đến ab, bc, ca













