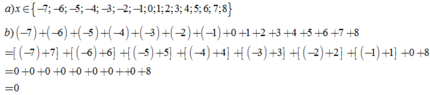Câu 8:Tìm các số biết

Những câu hỏi liên quan
a) Tìm các số nguyên x, biết: - 8 < x ≤ 8
b) Tính tổng các số tìm được ở câu a.
a, Tìm các số nguyên x biết -8 < x ≤ 8
b, Tính tổng các số tìm được ở câu a
a, x ∈ {-7;-6;-5;-4;-3;-2;-1;0;1;2;3;4;5;6;7;8}
b, (-7)+(-6)+(-5)+(-4)+(-3)+(-2)+(-1)+0+1+2+3+4+5+6+7+8
=[(-7)+7]+[(-6)+6]+[(-5)+5]+[(-4)+4]+[(-3)+3]+[(-2)+2]+[(-1)+1]+0+8
= 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 8
= 8
Đúng 0
Bình luận (0)
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 8 9 còn câu B thì cộng mấy số này vào
Câu 8: Tìm số nguyên x, biết:
a) 3x – 5 = -7 – 13
b) /x/ - 10 = -3
Câu 9: Liệt kê và tính tổng tất cả các số nguyên x, biết: -8 < x < 9
b) /x/ - 10 = -3
=> |x|=-3 + 10
|x|=7
=> x = 7 hoặc x= -7
a) 3x – 5 = -7 – 13
3x-5= -20
3x=-20+5
3x=-15
x=-15:3
x=-5
Câu 9 :
Ta có : -8 < x < 9 => \(x=\left\{\pm7;\pm6;\pm5;\pm4;...;8\right\}\)
Đặt \(S=\left(-7\right)+\left(-6\right)+...+8\)
=> \(S=\left(-7\right)+\left(-6\right)+\left(-5\right)+...+8\)
\(=\left[\left(-7\right)+7\right]+\left[\left(-6\right)+6\right]+...+8\)
\(=0+0+0+...+8\)
\(\Rightarrow s=8\)
Vậy S= 8
Nhờ các bạn giải giùm câu này :
Tìm đa thức f(x) có hệ số là các số tự nhiên nhỏ hơn 8 biết f(8)=1995
A) tìm số tự nhiên n nhỏ nhất n khác 0 biết rằng n chia hết cho 8 và 18 Câu B tìm các bội chung nhỏ hơn 150 của 12,30 Câu C tìm số tự nhiên n , biết rằng n chia hết cho 12,14,16 và 200<n<400
Câu 4. Tìm các số nguyên x và y biết:
a) (x-2)(2y+1)=8 b) (8-x)(4y+1)=20
2)a) vì 8 = 8.1 = 1.8 = 2.4 = 4.2
Vì 2y + 1 là số lẻ nên chỉ có 1 phương án là:
2y + 1 = 1 và x - 2 = 8 => y = 0 và x = 10
2b) 20 = 20 . 1 = 1 . 20 = 2.10 = 10.2 = 4.5 = 5.4
Mà 4y + 1 là số lẻ nên chỉ có thể có 2 trường hợp sau:
+) 4y + 1 = 1 và 8 - x = 20 => y = 0 và x = -12
+) 4y + 1 = 5 và 8 - x = 4 => y = 1 và x = 4
bạn phi công lái máy bay làm đúng rồi
Câu 1:Tính tổng của các số có 3 chữ số,các số đều chia 5 dư 3.
Câu 2:Tổng của 2 số lẻ là 98.Tìm số lớn biết giữa chúng có sáu số chẵn.
Câu 3:Tìm 1 số biết số đó chia 8 dư 5,chia 12 dư 1,hai thương hơn kém nhau 13 đơn vị.
Câu 4:Có bao nhiêu số có 4 chữ số khác nhau viết bởi các chữ số:0,1,2,3,4,5,6.
Câu 1: Tìm hai số biết tổng là 2009 và hiệu là 163.Câu 2: Tìm số tự nhiên bé nhất có tổng các chữ số là 15.Câu 3: Tìm số tự nhiên bé nhất có các chữ số khác nhau mà tổng các chữ số là 20.Câu 4: Tìm STN lớn nhất có các chữ số khác nhau mà tổng các chữ số là 10.Câu 5: Tìm STN lớn nhất có các chữ số khác nhau mà tổng các chữ số là 12.Câu 6: Tìm 2 số tự nhiên liên tiếp có tổng là 215.Câu 7: Tìm 2 số tự nhiên liên tiếp có tổng là 419.Câu 8: Tìm 2 số tự nhiên liên tiếp có tổng là 2009.Câu 9: Tìm 2 số...
Đọc tiếp
Câu 1: Tìm hai số biết tổng là 2009 và hiệu là 163.
Câu 2: Tìm số tự nhiên bé nhất có tổng các chữ số là 15.
Câu 3: Tìm số tự nhiên bé nhất có các chữ số khác nhau mà tổng các chữ số là 20.
Câu 4: Tìm STN lớn nhất có các chữ số khác nhau mà tổng các chữ số là 10.
Câu 5: Tìm STN lớn nhất có các chữ số khác nhau mà tổng các chữ số là 12.
Câu 6: Tìm 2 số tự nhiên liên tiếp có tổng là 215.
Câu 7: Tìm 2 số tự nhiên liên tiếp có tổng là 419.
Câu 8: Tìm 2 số tự nhiên liên tiếp có tổng là 2009.
Câu 9: Tìm 2 số chẵn liên tiếp có tổng là 338.
Câu 10: Tìm 2 số chẵn liên tiếp có tổng là 694.
câu 1:số lớn 1086 số bé:923
câu 2:69
câu 3:389
câu 4:19
câu 5:39
câu 6: 107 và 108
câu 7:209 và 210
câu 8:1004 và 1005
câu 9:168 và 170
câu 10: 346 và 348
Đúng 0
Bình luận (0)
câu 1: số lớn 1068
số bé 923
câu 2: 69
câu 3: 389
câu 4: 43210
câu 5: 54210
câu 6: số bé 107
số lớn 108
câu 7: số bé 209
số lớn 210
câu 8: số bé 1004
số lớn 1005
câu 9: số bé 168
số lớn 170
câu 10: số bé 346
số lớn 348
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 6. Cho a3 + b3 2. Tìm giá trị lớn nhất của biểu thức: N a + b.Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| |a - b|Câu 9.a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4ab) Cho a, b, c 0 và abc 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8Câu 10. Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2)b) (a + b + c)2 ≤ 3(a2 + b2 + c2)Câu 11. Tìm các giá trị của x sao cho:a) |2x – 3| |1 – x|b) x2 – 4x ≤ 5c) 2x(2x –...
Đọc tiếp
Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|
Câu 9.
a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
Câu 10. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
Câu 11. Tìm các giá trị của x sao cho:
a) |2x – 3| = |1 – x|
b) x2 – 4x ≤ 5
c) 2x(2x – 1) ≤ 2x – 1.
Câu 12. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 13. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Câu 9:
\(a,\left(a+1\right)^2\ge4a\\ \Leftrightarrow a^2+2a+1\ge4a\\ \Leftrightarrow a^2-2a+1\ge0\\ \Leftrightarrow\left(a-1\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=1\)
\(b,\) Áp dụng BĐT cosi: \(\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge2\sqrt{a}\cdot2\sqrt{b}\cdot2\sqrt{c}=8\sqrt{abc}=8\)
Dấu \("="\Leftrightarrow a=b=c=1\)
Câu 10:
\(a,\left(a+b\right)^2\le2\left(a^2+b^2\right)\\ \Leftrightarrow a^2+2ab+b^2\le2a^2+2b^2\\ \Leftrightarrow a^2-2ab+b^2\ge0\\ \Leftrightarrow\left(a-b\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b\)
\(b,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\le3a^2+3b^2+3c^2\\ \Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
Câu 13:
\(M=\left(a^2+ab+\dfrac{1}{4}b^2\right)-3\left(a+\dfrac{1}{2}b\right)+\dfrac{3}{4}b^2-\dfrac{3}{2}b+2021\\ M=\left[\left(a+\dfrac{1}{2}b\right)^2-2\cdot\dfrac{3}{2}\left(a+\dfrac{1}{2}b\right)+\dfrac{9}{4}\right]+\dfrac{3}{4}\left(b^2-2b+1\right)+2018\\ M=\left(a+\dfrac{1}{2}b-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\left(b-1\right)^2+2018\ge2018\\ M_{min}=2018\Leftrightarrow\left\{{}\begin{matrix}a+\dfrac{1}{2}b=\dfrac{3}{2}\\b=1\end{matrix}\right.\Leftrightarrow a=b=1\)
Đúng 3
Bình luận (0)
Câu 6:
$2=(a+b)(a^2-ab+b^2)>0$
$\Rightarrow a+b>0$
$4(a^3+b^3)-N^3=4(a^3+b^3)-(a+b)^3$
$=3(a^3+b^3)-3ab(a+b)=(a+b)(a-b)^2\geq 0$
$\Rightarrow N^3\leq 4(a^3+b^3)=8$
$\Rightarrow N\leq 2$
Vậy $N_{\max}=2$
Đúng 5
Bình luận (0)
Câu 7:
BĐT $\Leftrightarrow a^3+b^3\geq ab(a+b)$
$\Leftrightarrow a^3+b^3-ab(a+b)\geq 0$
$\Leftrightarrow (a-b)^2(a+b)\geq 0$ (luôn đúng với mọi $a,b,c>0$)
Vậy ta có đpcm
Dấu "=" xảy ra khi $a=b>0$, $c$ dương bất kỳ.
Đúng 5
Bình luận (0)
Xem thêm câu trả lời
Câu 1: Cho hàm số y = 2x\(^2\)
a) Hãy lập bảng tính các giá trị f(-5), f(-3), f(0), f(3), f(5)
b) Tìm x biết f(x) = 8, f(x) = 6 - 4\(\sqrt{2}\)
Câu 2: Cho hàm số y = f(x) = \(\dfrac{1}{3}x^2\)
Tìm các giá trị của x, biết rằng \(y=\dfrac{1}{27}\). Cũng câu hỏi tương tự với y = 5
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
Đúng 2
Bình luận (0)