nêu bạn thuc su muon giup thi vẽ hinh to se giup 

http://olm.vn/hoi-dap/question/36403.html
Bạn copy link trên vào google và enter là được

sai đề rồi hay sao ấy bạn

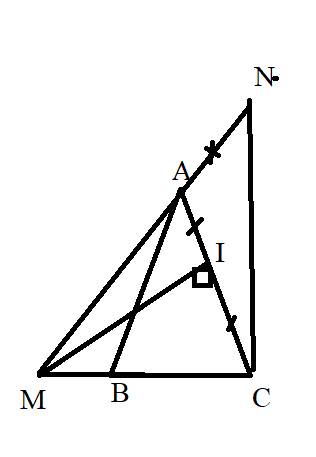
cho tam giác cân ABC có góc A = 45 độ,AB=AC.từ trung điểm I của cạnh AC kẻ đường vuông góc vs AC cắt đường thẳng BC ở M.trên tia đối của tia AM lấy điểm N sao cho AN=BM. cmr:

a] góc AMC=góc ABC

b] tam giác ABM= tam giác CAN

c] tam giác MNC vuông cân ở C

Đề bài yêu cầu gì vậy bạn?

bị thiếu đề phải ko bn!!!

không có câu hỏi sao trả lời???

Trả lời:

Tam giác AIM = tam giác CIM ( ch-chg)

nên MA=MC. tam giác AMC cân tại đỉnh M. Tam giác MAC và tam giác ABC là tam giác cân lại có chung gióc C nên góc ở đỉnh của chúng bằng nhau

Vậy góc AMC = góc BAC.

Ta có : ABMˆ+ABCˆ=180ABM^+ABC^=180 và CANˆ+CAMˆ=180CAN^+CAM^=180 ( vì cùng kề bù)

do đó: góc ABM = góc CAM.

Vậy tam giác ABM= tam giác CAN (c.g.c)

=> CN=AM mà AM=CM nên suy ra CM=CN. Tam giác MCN cân tại C

Tam giác ABC cân tại A có góc BAC =45

=> ACBˆ=180−452=67^o30′ACB^=180−452=67^o30′

Mà ACBˆ=MACˆACB^=MAC^ nên MABˆ=67^o30′

Khi đó MABˆ=MACˆ−BACˆ=67^o30′−450=22^o30′MAB^=MAC^−BAC^=67^o30′−45⁰=22^o30′

⇒ACNˆ=22⁰30′⇒ACN^=22^o30′

MCNˆ=MCAˆ+ACMˆ=67⁰30′+22^o30′=90^oMCN^=MCA^+ACM^=67^o30′+22^o30′=90^o

\(\Rightarrow\)Tam giác CMN vuông cân ở C

                                    ~Học tốt!~

a: Xét ΔMAC có 

MI là đường cao

MI là đường trung tuyến

Do đó: ΔMAC cân tại M

=>\(\widehat{AMC}=180^0-2\cdot\widehat{ACM}=180^0-2\cdot\widehat{ACB}\left(1\right)\)

ΔABC cân tại A

=>\(\widehat{BAC}=180^0-2\cdot\widehat{ACB}\left(2\right)\)

Từ (1) và (2) suy ra \(\widehat{AMC}=\widehat{BAC}\)

b:

ΔABC cân tại A

=>\(\widehat{ABC}=\widehat{ACB}\)

ΔMAC cân tại M

=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)

 \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)

=>\(\widehat{ABM}=180^0-\widehat{ABC}=180^0-\widehat{ACB}\left(3\right)\)

\(\widehat{CAN}+\widehat{CAM}=180^0\)(hai góc kề bù)

=>\(\widehat{CAN}+\widehat{ACB}=180^0\)

=>\(\widehat{CAN}=180^0-\widehat{ACB}\left(4\right)\)

Từ (3) và (4) suy ra \(\widehat{ABM}=\widehat{CAN}\)

Xét ΔABM và ΔCAN có

AB=CA

\(\widehat{ABM}=\widehat{CAN}\)

BM=AN

Do đó;ΔABM=ΔCAN

c: ΔABM=ΔCAN

=>NC=MA

mà MA=MC

nên NC=MC

\(\widehat{AMC}=\widehat{BAC}\)

mà \(\widehat{BAC}=45^0\)

nên \(\widehat{AMC}=45^0\)

Xét ΔCMN có CM=CN và \(\widehat{CMN}=45^0\)

nên ΔCMN vuông cân tại C