cho hình bình hành ABCD có M,N là trung điểm của AB và CD , AN và CM căt sBD ở E và F . Chứng minh :
a) AM=CN và tứ giác AMCN là hình bình hành
b) F là trung điểm của BE và E là trùn điểm của DF

Những câu hỏi liên quan
cho hình bình hành ABCD có m,n là trung điểm của AB và CD, AN và CM cắt BD ở EF. CM
a)AM=CN và tứ giác AMCN là hình bình hành
b)F là trung điểm của BE
c)DE=EF=FB
a, AB=CD(các cạnh đối bằng nhau theo từng đôi)
Mà M,N lần lượt là trung điểm AB, CD=> AM=BM=CN=DN
=>AM=CN
Vì AM=CN và AM//CN(AB//CD)=> AMCN là hình bình hành.
b, AMCN là hình bình hành=>AN//MC=>AE//MF
Tam giác ABE có: AE//MF và MA=MB=> EF=FB(tính chất đường trung bình) (1) => F là trung điểm BE.
c, AN//MC=>EN//FC
Tam giác DFC có: EN//FC và ND=NC=> DE=EF(tính chất đường trung bình) (2)
Từ (1) và (2)=>DE=EF=FB.
Dành cho những học siinh không làm được bài mò vào xem nè! Còn đúng hay sai mình không đảm bảo nha!!!
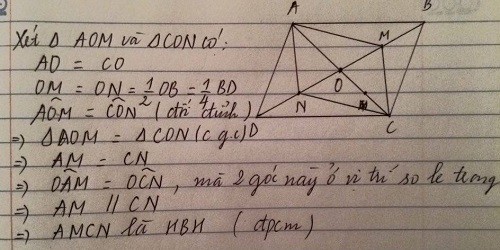
Cho hình bình hành ABCD , O là giao điểm của 2 đường chéo , M và N là trung điểm của OD và OB
E là giao điểm của AM và CD ,
F là giao điểm của CN và AB
a) Chứng minh a tứ giác AMCN là hình bình hành
b) Chứng minh b AECF là hình bình hành
a)Ta có O giao điểm AC và BD trong hình bình hành ABCD (gt)
=> O là trung điểm AC và BD.
=> OD=OB
Mà OM=MD=\(\frac{1}{2}\)OD; ON=BN=\(\frac{1}{2}\)OB => OM=ON=OD=OB.
Xét hình bình hành ABCD có O trung điểm AC (hbh ABCD) và O trung điểm MN (OM=ON)
=> đpcm (điều phải chứng minh)
b) C/m tam giác ACE=ACF (cgc)(AC chung; \(\angle EAC=\angle FCA\) do song song; và cũng như vây với \(\angle ECA=\angle CAF\))
=>AE=FC mà \(AE \parallel FC\) do ăn theo hbh AMCN => đpcm
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo. Gọi M,N theo thứ tự là trung điểm của OB và OD. Gọi E là giao điểm của AM và CD, F là giao điểm của CN và AB
a) Chứng minh tứ giác AMCN là hình bình hành
b) Tứ giác AECF là hình gì? Vì sao?
c) Chứng minh E và F đối xứng nhau qua O
d) Chứng minh EC = 2DE
O là giao điểm của hai đường chéo AC,BD(gt)
=> AO=OC, OD=OB (vì ABCD là hình bình hành)
Lại có;
E là trung điểm của OD(gt)
=> OE=1/2.OD
F là trung điểm của OB(gt)
=> OF=1/2.OB
Mà OD=OB (cmt)
=> OE=OF
Tứ giác AFCE có: OA=OC(cmt) và OE=OF(cmt)
=> O là giao điểm của hai đường chéo AC,EF cắt nhau tại trung điểm mỗi đoạn
=> AFCE là hình bình hành
=> AE//CF (vì AE, CF là hai cạnh đối nhau)
Có AE//CF (cmt) => EK// CF (vì K thuộc AE)
Từ O vẽ đường thẳng cắt CD tại H sao cho OH//EK//CF
Xét tam giác DOH có: E là trung điểm của OD
EK//OH (theo cách vẽ đường thẳng OH)
=> K là trung điểm của DH
=> DK=KH (1)
Xét hình thang EKCF có: O là trung điểm của EF (theo câu a)
OH//EK//CF (theo cách vẽ đường thẳng OH)
=> H là trung điểm của KC
=> KH=HC (2)
Từ (1) và (2) => DK=KH=HC
Lại có: KC=KH+HC => KC= DK+DK (vì DK=KH=HC)
=> KC=2DK => DK=1/2KC
Đúng 3
Bình luận (0)
Bài 1 Cho hình bình hành ABCD; O là giao điểm 2 đường chéo Gọi M,N lần lượt là trung điểm của OD và OB; AM cắt CD tại E CN cắt AB tại F
a) CM tứ giác AMCN, AECF là hình bình hành
b) E và F có đối xứng qua O không tại sao?
c) Chứng minh DE=1/2 EC
Cho hình bình hành ABCD có M,N là trung điểm của AB và CD,AN và CM cắt BD ở E và F.
a)Chứng minh AMCN là hình bình hành
b)Chứng minh AC;MN;EF đồng quy
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. M,N là trung điểm của OD và OB. E là giao đeliểm của AM và CD. F là giao điểm của CN và AB
CMR: a, Tứ giác AMCN là hình bình hành
b, Tứ giác AECF là hình bình hành
c, DE bằng một phần hai EC
Mn ơi ai giúp mk đi mk đg gấp lắm cầu xin đó 🙏🙏🙏hu hu hu hu
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình bình hành ABCD, M và N là trung điểm của AB và CD.
a/ Chứng minh: AMCN là hình bình hành.
b/ BD cắt AN ở E, cắt CM ở F. Chứng minh: DE = EF = FB.
Cho hình bình hành ABCD , hai đường chéo cắt nhau taij O.Lấy M,N lần lượt là trung điểm của OD , OB,E là giao điểm của AM và CD,F là giao điểm của CN và AB. a.chứng minh AMCN là hình bình hành b. Chứng minh DE=BF
a:
ABCD là hbh
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
OM=OD/2
ON=OB/2
mà OD=OB
nên OM=ON
=>O là trung điểm của MN
Xét tứ giác AMCN có
O là trung điểm chung của AC và MN
=>AMCN là hbh
b: Xét tứ giác AFCE có
AF//CE
AE//CF
=>AFCE là hbh
=>AF=CE
AF+FB=AB
CE+ED=CD
mà AF=CE và AB=CD
nên FB=ED
Đúng 1
Bình luận (0)
cho hình bình hành ABCD (với AB>CD) Gọi M và N theo thứ tự là trung điểm của AB và CD A) Chứng minh AN=CM B) Chứng minh tứ giác AMCN là hình bình hành C) Chứng minh AM//CM