cho tam giác MNP cân tại M .Kẻ NH vuông góc với MP.Gọi D thuộc NP ,DF vuông góc với MN.CMR DE+DF=NH

Những câu hỏi liên quan
cho tam giacs MNP cân tại M. Kẻ NH vuông góc với MP.gọi D là một điểm thuộc canh đáy NP, kẻ DE vuông góc MP, DE vuông góc với MP, DF vuông góc MN. CM: DE+ DF= NH
Cho tam giác MNP cân tại M. Kẻ NH vuông góc NP. Gọi D là Một điểm thuộc cạnh đáy NP, kẻ DE vuông góc MP, DF vuông góc MN. Chứng minh DE+ DF= NH Các bạn giải giúp mình nhé ktra nhưng cô chưa chữa.
thiếu điều kiện, Cm DE+DF=NH thì phải cho giới hạn điểm H chứ
Đúng 0
Bình luận (0)
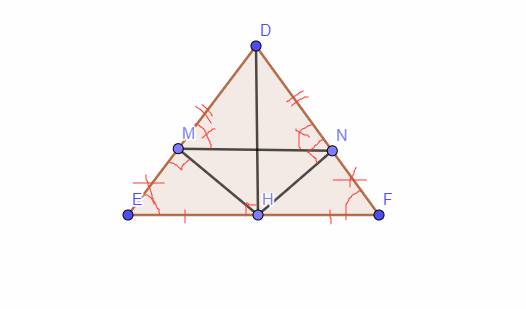
Cho tam giác DEF cân tại D. Kẻ DH vuông góc EF (H thuộc EF) Chứng minh tam giác HED bằng tam giác HFD Kẻ HM vuông góc DE (M thuộc DE) và HN vuông góc DF (N thuộc DF). Chứng minh tam giác DMN cân tại D và MN song song với EF
\(\text{#TNam}\)
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`
Đúng 2
Bình luận (0)
Cho tam giác DEF cân tại D. Kẻ DH vuông góc với EF (H thuộc EF). Kẻ HM vuông góc với DE (M thuộc DE) và HN vuông góc với DF (N thuộc DF). Góc HDE = góc HDF. CM:
a) HM = HN.
b) Tam giác HME = tam giác HNF.
lưu ý hình ảnh chỉ mang t/c minh họa ; vui lòng k vẽ theo
xét \(\Delta DHM\)VÀ \(\Delta DHN\)
DH-CẠNH CHUNG
\(\widehat{HDM}=\widehat{HDN}\left(gt\right)\)
\(\widehat{DMH}=\widehat{DNH}=90^o\left(gt\right)\)
=> \(\Delta DHM=\Delta DHN\)
=>HM = HN.
b) xét tam giác DEF cân tại D
=> \(\widehat{DEF}=\widehat{DFE}\)(T/C TAM GIÁC CÂN )
=>\(\widehat{MEH}=\widehat{NFH}\)
XÉT \(\Delta MEH\)VÀ \(\Delta NFH\)
\(\widehat{EMH}=\widehat{FNH}=90^o\left(gt\right)\)
\(\widehat{MEH}=\widehat{NFH}\left(cmt\right)\)
\(HM=HN\left(cmt\right)\)
=> \(\Delta MEH=\Delta NFH\)
Cho tam giác DEF cân tại D. Kẻ DH vuông góc với EF (H thuộc EF). Kẻ HM vuông góc với DE (M thuộc DE) và HN vuông góc với DF (N thuộc DF). Góc HDE = góc HDF. CM:
a) HM = HN.
b) Tam giác HME = tam giác HNF.
a) Xét 2 tam giác vuông: \(\Delta MDH\)và \(\Delta NDH\)có:
\(\widehat{MDH}=\widehat{NDH}\left(gt\right)\)
\(HD\)cạnh chung
\(\Rightarrow\Delta MDH=\Delta NDH\left(ch-gn\right)\)
\(\Rightarrow HM=HN\)( 2 cạnh tương ứng)
b) Ta có: \(DE=DF\)( vì tam giác DEF cân tại D )
Hay \(DM+ME=DN+NF\)
mà \(DM=DN\)( 2 cạnh tương ưng của tam giác MDH và tam giác NDH )
\(\Rightarrow ME=NF\)
Xét \(\Delta HME\)và \(\Delta HNF\)có:
\(\widehat{HME}=\widehat{HNF}\left(=90^o\right)\)
\(ME=NF\left(cmt\right)\)
\(\widehat{MEH}=\widehat{NFH}\) ( vì tam giác DEF cân tại D)
\(\Rightarrow\Delta HME=\Delta HNF\left(g-c-g\right)\)
hok tốt!!
Cho tam giác MNP vuông tại N. Gọi D là trung điểm của MP. Từ D kẻ DE vuông góc với MN (M thuộc MN), DF vuông góc NP ( F thuộc NP). Trên tia DF lấy điểm I sao cho F là trung điểm của DI
a) Tứ giác NEDF là hình gì? Vì sao/
b) Chứng mình F là trung điểm của NP
a ) Xét ◇DENF có :
Góc N = Góc F = Ê = 90°
\(\Rightarrow\)◇DENF là hình chữ nhật
b ) Trong \(\Delta\)MNP có : ND là đường trung tuyến
\(\Rightarrow\)ND = DP ( vì đường trung tuyến bằng nữa cạnh huyền )
Xét \(\Delta\)NDF và \(\Delta\)PDF có :
ND = DP ( cmt )Góc NFD = Góc PFD ( = 90° )DF : cạnh chung\(\Rightarrow\)\(\Delta\)NDF = \(\Delta\)PDF ( cạnh huyền - cạnh góc vuông )
\(\Rightarrow\)NF = PF ( 2 cạnh tương ứng )
\(\Rightarrow\)F là trung điểm NP

a) Xét tứ giác NEDF có +) \(\widehat{ENF}=90^0\)(tam giác MNP vuông tại N)
+) \(\widehat{DFN}=90^0\)(DF vuông góc NP)
+) \(\widehat{DEN}=90^0\)(DE vuông góc MN)
\(\Rightarrow\)tứ giác NEDF là hình chữ nhật
b) Xét \(\Delta DFN\)và \(\Delta DFP\)có:
DF : cạnh chung
DN = DP ( Do ND là trung tuyến của tam giác vuông MNP)
Do đó \(\Delta DFN\)\(=\Delta DFP\left(ch-cgv\right)\)
\(\Rightarrow NF=PF\)
Suy ra F là trung điểm của NP (đpcm)
Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC. Gọi D là một điểm thuộc cạnh đấy BC. Kẻ DE vuông góc với AC, DF vuông góc với AB. Chứng minh DE+DF=BH
Em tham khảo nhé
Kẻ DK vuông góc với BH
Xét từ giác DKHE có góc K = góc E = góc H = 90 độ => tứ giác DKHE là HCN
=> DE = KH
DK//AC => góc KDB = góc ACB(đồng vị)
Mà góc ACB = góc ABC (tam giác ABC cân tại A)
=> góc KDB = góc FBC
Xét tam giác BDF và tam giác DBK có
Góc BFD = góc DKB = 90 độ
BD chung
góc DBF = góc BDK
=> tam giác BFD = tam giác DBK (g.c.g)
=> BK = DF
Ta có BH = BK + KH
Mà BK = DF, KH = DE
=> BH = DE + DF (đpcm)
Đúng 2
Bình luận (1)
cho tam giác ABC cân tại A , kẻ BH vuông góc với AC . gọi D là một điểm thuộc cạnh đáy BC . kẻ DE vuông góc với AC , DF vuông góc với AB . cm rằng DE+DF=BH
Cho tam giác ABC cân tại A, kẻ BH vuông góc AC. Gọi D là một điểm thuộc cạnh đáy BC. Kẻ DE vuông góc với AC, DF vuông góc với AB. Chứng minh rằng DE+DF= BH




















