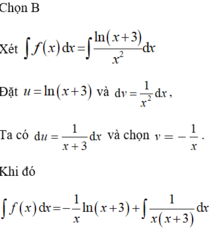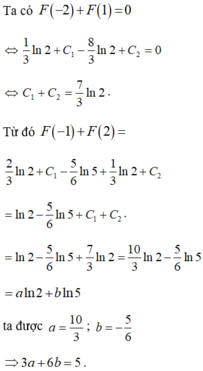Cho số hữu tỷ x thỏa mãn x^2 + 2x là một số nguyên. Chứng minh x là một số nguyên.

Những câu hỏi liên quan
Cho số hữu tỷ x thỏa mãn x^2 + 2x là một số nguyên. Chứng minh x là một số nguyên.
Tìm tất cả các số hữu tỷ x > 0 thỏa mãn 2x và 5/x đều là số nguyên.
\(x=\frac{a}{b};a,b>0;\left(a,b\right)=1\).
\(\frac{5}{x}=\frac{5b}{a}\inℤ\Rightarrow a\inƯ\left(5\right)=\left\{1,5\right\}\).(vì \(\left(a,b\right)=1\))
Với \(a=1\):
\(2x=\frac{2}{b}\inℤ\Rightarrow b\inƯ\left(2\right)=\left\{1,2\right\}\)
Thử lại \(x=1,x=\frac{1}{2}\)đều thỏa mãn.
Với \(a=5\):
\(2x=\frac{10}{b}\Rightarrow b\inƯ\left(10\right)=\left\{1,2,5,10\right\}\)
\(\left(a,b\right)=1\)nên \(b\in\left\{1,2\right\}\).
Thử lại \(x=5,x=\frac{5}{2}\)đều thỏa mãn.
Vậy \(x\in\left\{1,\frac{1}{2},5,\frac{5}{2}\right\}\).
2x và 5/x
2x luôn là số nguyên
Vậy để thỏa đề thì 5/x phải là số nguyên
=> 5 chia hết cho x
x thuộc ước của 5
mà x > 0
Vậy x = 1 hoặc x = 5
Bài 1. Tìm các số thực x thỏa mãn:a. |3 − |2x − 1|| x − 1b. |x − 1| + |2x − 2| + |4x − 4| + |5x − 5| 36c. |x − 2| + |x − 3| + ... + |x − 9| 1 − xBài 2. Cho các số nguyên a, b, c thỏa mãn a + b + c 0. Chứng minh rằng: |a| + |b| + |c| là một sốchẵn.Bài 3. Cho các số nguyên a, b, c thỏa mãn a + b + c 2020. Tổng A |a − 1| + |b + 1| + |c − 2020|có thể bằng 2021 được không? Vì sao?Bài 4. Cho các số nguyên a, b, c. Chứng minh rằng: |a − 2b| + |4b − 3c| + |c − 3a| là một số chẵn.
Đọc tiếp
Bài 1. Tìm các số thực x thỏa mãn:
a. |3 − |2x − 1|| = x − 1
b. |x − 1| + |2x − 2| + |4x − 4| + |5x − 5| = 36
c. |x − 2| + |x − 3| + ... + |x − 9| = 1 − x
Bài 2. Cho các số nguyên a, b, c thỏa mãn a + b + c = 0. Chứng minh rằng: |a| + |b| + |c| là một số
chẵn.
Bài 3. Cho các số nguyên a, b, c thỏa mãn a + b + c = 2020. Tổng A = |a − 1| + |b + 1| + |c − 2020|
có thể bằng 2021 được không? Vì sao?
Bài 4. Cho các số nguyên a, b, c. Chứng minh rằng: |a − 2b| + |4b − 3c| + |c − 3a| là một số chẵn.
Số hữu tỉ x thỏa mãn x2-2 là số nguyên. CMR: x cũng là một số nguyên
Ta có: \(x^2-2\in Z,-2\in Z\)
\(\Rightarrow x^2\in Z\Rightarrow x\in Z\)
Đúng 0
Bình luận (0)
Vì \(x^2-2\) là số nguyên
mà 2 là số nguyên
nên \(x^2\) là số nguyên
hay x là số nguyên
Đúng 0
Bình luận (0)
Số hữu tỉ x thỏa mãn x2+2 là số nguyên. CMR: x cũng là một số nguyên
x^2 + 2 nguyên mà 2 nguyên suy ra x^2 nguyên mà x hữu tỉ nên nếu x không nguyên thì x^2 không nguyên ( cái này là do căn 2 của 1 số nguyên là 1 số nguyên hoặc 1 số vô tỉ ) nên x nguyên.
Cho x, y là số hữu tỉ khác 1 thỏa mãn: \(\dfrac{1-2x}{1-x}+\dfrac{1-2y}{1-y}=1\)
Chứng minh \(M=x^2+y^2-xy\) là bình phương của một số hữu tỉ
Bài 1. Tìm các số thực x thỏa mãn:a. |3 − |2x − 1|| x − 1b. |x − 1| + |2x − 2| + |4x − 4| + |5x − 5| 36c. |x − 2| + |x − 3| + ... + |x − 9| 1 − xBài 2. Cho các số nguyên a, b, c thỏa mãn a + b + c 0. Chứng minh rằng: |a| + |b| + |c| là một sốchẵn.Bài 3. Cho các số nguyên a, b, c thỏa mãn a + b + c 2020. Tổng A |a − 1| + |b + 1| + |c − 2020|có thể bằng 2021 được không? Vì sao?Bài 4. Cho các số nguyên a, b, c. Chứng minh rằng: |a − 2b| + |4b − 3c| + |c − 3a| là một số chẵn.Các thần đồng đâu...
Đọc tiếp
Bài 1. Tìm các số thực x thỏa mãn:
a. |3 − |2x − 1|| = x − 1
b. |x − 1| + |2x − 2| + |4x − 4| + |5x − 5| = 36
c. |x − 2| + |x − 3| + ... + |x − 9| = 1 − x
Bài 2. Cho các số nguyên a, b, c thỏa mãn a + b + c = 0. Chứng minh rằng: |a| + |b| + |c| là một số
chẵn.
Bài 3. Cho các số nguyên a, b, c thỏa mãn a + b + c = 2020. Tổng A = |a − 1| + |b + 1| + |c − 2020|
có thể bằng 2021 được không? Vì sao?
Bài 4. Cho các số nguyên a, b, c. Chứng minh rằng: |a − 2b| + |4b − 3c| + |c − 3a| là một số chẵn.
Các thần đồng đâu hết rùi
Giải hộc cái bài nào
Giả sử F(x) là một nguyên hàm của hàm số thỏa mãn F(-2) + F(1) 0 và F(-1) + F(2) 0, với a,b là các số hữu tỷ. Giá trị của 3a+6b bằng A. -4 B. 5 C. 0 D. -3
Đọc tiếp
Giả sử F(x) là một nguyên hàm của hàm số 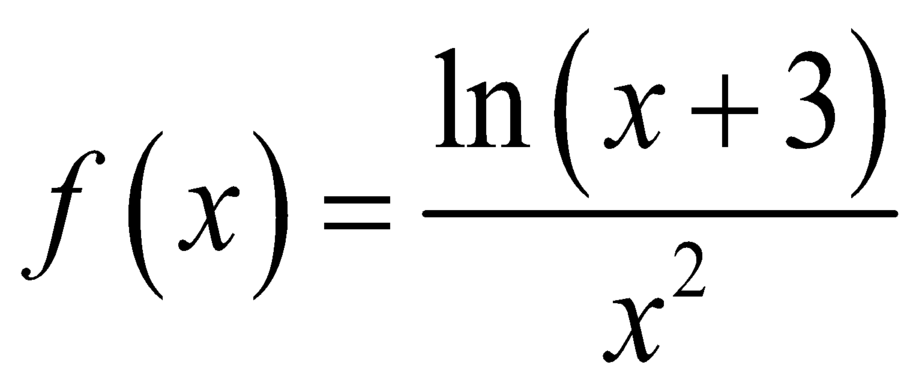 thỏa mãn F(-2) + F(1) = 0 và F(-1) + F(2) = 0, với a,b là các số hữu tỷ.
thỏa mãn F(-2) + F(1) = 0 và F(-1) + F(2) = 0, với a,b là các số hữu tỷ.
Giá trị của 3a+6b bằng
A. -4
B. 5
C. 0
D. -3
Cho các số nguyên x,y,z khác không, thỏa mãn x+y+z=0.
Chứng minh rằng căn (1/ x^2 + 1/y^2 + 1/z^2) là số hữu tỉ
Ta có:
\(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+0}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2\left(x+y+z\right)}{xyz}}\)
\(=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2}{xy}+\dfrac{2}{yz}+\dfrac{2}{zx}}=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}\)
\(=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\) là số hữu tỉ
Đúng 0
Bình luận (0)