Cho biểu thức B= 3 cănX trên 2cănX +1 Tìm X để giá trị của B là một số nguyên

Những câu hỏi liên quan
Cho biểu thức B= 3 cănX trên cănX +1
Tìm X để giá trị của B là một số nguyên
cho A=cănx/căn(x+3)+2cănx/căn(x-3)-3x+9/x-9,với x lớn hơn bằng 0,x khác 9
a rút gọn biểu thức A
b tìm x để a=1/3
c tìm giá trị lớn nhất của A
Bạn vui lòng viết đề bằng công thức toán để được hỗ trợ tốt hơn.
Đúng 2
Bình luận (3)
`a)A=sqrtx/(sqrtx+3)+(2sqrtx)/(sqrtx-3)-(3x+9)/(x-9)(x>=0,x ne 9)`
`=(sqrtx(sqrtx-3)+2sqrtx(sqrtx+3)-3x-9)/(x-9)`
`=(x-3sqrtx+2x+6sqrtx-3x-9)/(x-9)`
`=(3sqrtx-9)/(x-9)`
`=(3(sqrtx-3))/((sqrtx-3)(sqrtx+3))`
`=3/(sqrtx+3)`
`b)A=1/3`
`<=>3/(sqrtx+3)=1/3`
`<=>sqrtx+3=9`
`<=>sqrtx=6`
`<=>x=36(tm)`
`c)A=3/(sqrtx+3)`
`sqrtx+3>=3>0`
`=>A<=3/3=1`
Dấu "=" xảy ra khi `x=0`
Đúng 3
Bình luận (0)
Cho hàm số: y= f(x) = -2x+5 (1)
a)Vẽ đô thị hàm số (1) trên mặt phẳng tọa độ
b)Tìm tọa độ giao điểm I của hai hàm số y= -2x+5 và y= x-1 bằng phương pháp tính
Đúng 0
Bình luận (0)
cho bieu thuc A =x/x-4+1/cănx-2+1/cănx+1 a,rút gọn b,tính giá trị của A khi x=25 c, tìm các giá trị của x để A=-1/3 d,tìm các giá trị nguyên của x để A là các số nguyên
1. Cho biểu thức A sqrt{4-2x}a) Tìm điều kiện của x để biểu thức có nghĩa.b) Tìm giá trị của biểu thức khi x2, x0,x1,x-6,x-10.c) Tìm giá trị của biến x để giá trị của biểu thức bằng 0? Bằng 5? Bằng 10?2. Cho biểu thức P frac{9}{2sqrt{x}-3}a) Tìm điều kiện của X để biểu thức P xác định..b) Tính giá trị của biểu thức khi x4, x100c) Tìm giá trị của x để P1, P7d) Tìm các số nguyên x để giá trị của P cũng là một số nguyên.3. Cho biểu thức frac{2sqrt{x}+9}{sqrt{x}+1}a) Tìm điều kiện xác định của x để...
Đọc tiếp
1. Cho biểu thức A= \(\sqrt{4-2x}\)
a) Tìm điều kiện của x để biểu thức có nghĩa.
b) Tìm giá trị của biểu thức khi x=2, x=0,x=1,x=-6,x=-10.
c) Tìm giá trị của biến x để giá trị của biểu thức bằng 0? Bằng 5? Bằng 10?
2. Cho biểu thức P= \(\frac{9}{2\sqrt{x}-3}\)
a) Tìm điều kiện của X để biểu thức P xác định..
b) Tính giá trị của biểu thức khi x=4, x=100
c) Tìm giá trị của x để P=1, P=7
d) Tìm các số nguyên x để giá trị của P cũng là một số nguyên.
3. Cho biểu thức \(\frac{2\sqrt{x}+9}{\sqrt{x}+1}\)
a) Tìm điều kiện xác định của x để biểu thức Q được xác định.
b) Tính giá trị của biểu thức khi x=0,x=1,x=16.
c) Tìm giá trị của x để Q=1,Q=10.
d) Tìm các số nguyên x để giá trị của Q cũng là một số nguyên.
Giải hộ với ạ! Gấp lắm T.T
1) a) Căn thức có nghĩa \(\Leftrightarrow4-2x\ge0\Leftrightarrow2x\le4\Leftrightarrow x\le2\)
b) Thay x = 2 vào biểu thức A, ta được: \(A=\sqrt{4-2.2}=\sqrt{0}=0\)
Thay x = 0 vào biểu thức A, ta được: \(A=\sqrt{4-2.0}=\sqrt{4}=2\)
Thay x = 1 vào biểu thức A, ta được: \(A=\sqrt{4-2.1}=\sqrt{2}\)
Thay x = -6 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-6\right)}=\sqrt{16}=4\)
Thay x = -10 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-10\right)}=\sqrt{24}=2\sqrt{6}\)
c) \(A=0\Leftrightarrow\sqrt{4-2x}=0\Leftrightarrow4-2x=0\Leftrightarrow x=2\)
\(A=5\Leftrightarrow\sqrt{4-2x}=5\Leftrightarrow4-2x=25\Leftrightarrow x=\frac{-21}{2}\)
\(A=10\Leftrightarrow\sqrt{4-2x}=10\Leftrightarrow4-2x=100\Leftrightarrow x=-48\)
Đúng 0
Bình luận (0)
2) a) P xác định \(\Leftrightarrow x\ge0\)và \(2\sqrt{x}-3\ne0\Leftrightarrow\sqrt{x}\ne\frac{3}{2}\Leftrightarrow x\ne\frac{9}{4}\)
b) Thay x = 4 vào P, ta được: \(P=\frac{9}{2\sqrt{4}-3}=\frac{9}{1}=9\)
Thay x = 100 vào P, ta được: \(P=\frac{9}{2\sqrt{100}-3}=\frac{9}{17}\)
c) P = 1 \(\Leftrightarrow\frac{9}{2\sqrt{x}-3}=1\Leftrightarrow2\sqrt{x}-3=9\Leftrightarrow\sqrt{x}=6\Leftrightarrow x=36\)
P = 7 \(\Leftrightarrow\frac{9}{2\sqrt{x}-3}=7\Leftrightarrow2\sqrt{x}-3=\frac{9}{7}\)
\(\Leftrightarrow2\sqrt{x}=\frac{30}{7}\Leftrightarrow\sqrt{x}=\frac{15}{7}\Leftrightarrow x=\frac{225}{49}\)
d) P nguyên \(\Leftrightarrow9⋮2\sqrt{x}-3\)
\(\Leftrightarrow2\sqrt{x}-3\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)
Lập bảng:
| \(2\sqrt{x}-3\) | \(1\) | \(-1\) | \(3\) | \(-3\) | \(9\) | \(-9\) |
| \(\sqrt{x}\) | \(2\) | \(1\) | \(3\) | \(0\) | \(6\) | \(-3\) |
| \(x\) | \(4\) | \(1\) | \(9\) | \(0\) | \(36\) | \(L\) |
Vậy \(x\in\left\{1;4;9;0;36\right\}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1 : Tìm x, y : a, (x-5).(y+3)=10
b, x.y-x-y=1
Bài 2 : cho biểu thức 3/x-1
a, với điều kiện nào của x thì biểu thức là 1 phân số
b, tìm các giá trị nguyên của x để giá trị phân số là một số nguyên
Cho biểu thức:A=\(\dfrac{2x-1}{x+2}\)
a) Tìm số nguyên x để biểu thức A là phân số
b)Tìm các số nguyên x để biểu thức A có giá trị là 1 số nguyên
c)Tìm các số nguyên x để biểu thức A đạt giá trị lớn nhất,giá trị nhỏ nhất
A = \(\dfrac{2x-1}{x+2}\)
a, A là phân số ⇔ \(x\) + 2 # 0 ⇒ \(x\) # -2
b, Để A là một số nguyên thì 2\(x-1\) ⋮ \(x\) + 2
⇒ 2\(x\) + 4 - 5 ⋮ \(x\) + 2
⇒ 2(\(x\) + 2) - 5 ⋮ \(x\) + 2
⇒ 5 ⋮ \(x\) + 2
⇒ \(x\) + 2 \(\in\) { -5; -1; 1; 5}
⇒ \(x\) \(\in\) { -7; -3; -1; 3}
c, A = \(\dfrac{2x-1}{x+2}\)
A = 2 - \(\dfrac{5}{x+2}\)
Với \(x\) \(\in\) Z và \(x\) < -3 ta có
\(x\) + 2 < - 3 + 2 = -1
⇒ \(\dfrac{5}{x+2}\) > \(\dfrac{5}{-1}\) = -5 ⇒ - \(\dfrac{5}{x+2}\)< 5
⇒ 2 - \(\dfrac{5}{x+2}\) < 2 + 5 = 7 ⇒ A < 7 (1)
Với \(x\) > -3; \(x\) # - 2; \(x\in\) Z ⇒ \(x\) ≥ -1 ⇒ \(x\) + 2 ≥ -1 + 2 = 1
\(\dfrac{5}{x+2}\) > 0 ⇒ - \(\dfrac{5}{x+2}\) < 0 ⇒ 2 - \(\dfrac{5}{x+2}\) < 2 (2)
Với \(x=-3\) ⇒ A = 2 - \(\dfrac{5}{-3+2}\) = 7 (3)
Kết hợp (1); (2) và(3) ta có A(max) = 7 ⇔ \(x\) = -3
Đúng 1
Bình luận (0)
Tìm x để biểu thức sau là số nguyên: A= 2cănx/(x^2-2cănx+4)
Mọi người giúp mình vs ạ
Bài 1.Tìm GTLN của các biểu thức sau:
A=1/x^2+2x+3
B=4/x- cănx +5/4
C=(5cănx)/2(x- 3cănx+2)
Bài 2:Tìm GTNN của các biểu thức sau:
A= cănx -x+3
B=x+ cănx -7
C=-3/x^2-2x+3
D=-5/2x- 4cănx+5
E=(-2cănx)/6cănx -2x+3
sử dụng hằng đẳng thức là đc bạn
Bài 2: Cho biểu thức A=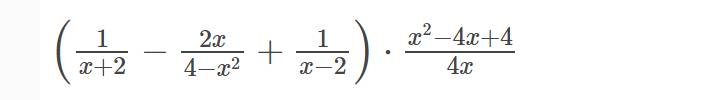
a) tìm điều kiện của A để xác định
b) Rút gọn biểu thức A
Câu 6: tìm các giá nguyên của x để để giá trị biểu thức 9x+4/3x+1 là một số nguyên
Câu 6:
ĐKXĐ: \(x\ne-\dfrac{1}{3}\)
Để \(\dfrac{9x+4}{3x+1}\in Z\) thì \(9x+4⋮3x+1\)
=>\(9x+3+1⋮3x+1\)
=>\(1⋮3x+1\)
=>\(3x+1\in\left\{1;-1\right\}\)
=>\(3x\in\left\{0;-2\right\}\)
=>\(x\in\left\{0;-\dfrac{2}{3}\right\}\)
mà x nguyên
nên x=0
Câu 2:
a: ĐKXĐ: \(x\notin\left\{2;-2;0\right\}\)
b: \(A=\left(\dfrac{1}{x+2}-\dfrac{2x}{4-x^2}+\dfrac{1}{x-2}\right)\cdot\dfrac{x^2-4x+4}{4x}\)
\(=\left(\dfrac{1}{x+2}+\dfrac{2x}{\left(x-2\right)\left(x+2\right)}+\dfrac{1}{x-2}\right)\cdot\dfrac{\left(x-2\right)^2}{4x}\)
\(=\dfrac{x-2+2x+x+2}{\left(x+2\right)\left(x-2\right)}\cdot\dfrac{\left(x-2\right)^2}{4x}\)
\(=\dfrac{4x\left(x-2\right)}{4x\left(x+2\right)}=\dfrac{x-2}{x+2}\)
Đúng 2
Bình luận (0)




















