+) Kẻ: AJ // CI //EF; I; J thuộc BD và M thuộc EF

Xét \(\Delta\)BAJ  có: FM // AJ 

=> \(\frac{BA}{BF}=\frac{BJ}{BM}\)

Xét  \(\Delta\)BCI có: ME // IC 

=> \(\frac{BC}{BE}=\frac{BI}{BM}\)

Từ hai điều trên => \(\frac{BA}{BF}+\frac{BC}{BE}=\frac{BJ}{BM}+\frac{BI}{BM}=\frac{BI+BJ}{BM}\)(1)

Xét \(\Delta\)AJO và \(\Delta\)CIO  có:

OA = OC ( ABCD là hình bình hành) 

^AOJ = ^COI ( đối đỉnh)

^AJO = ^CIO ( AJ // CI , so le trong )

=> \(\Delta\)AJO = \(\Delta\)CIO ( g-c-g)

=> JO = IO 

KHi đó BI + BJ = BO + OI + BO - JO  = 2 BO +  (IO - JO) = 2 BO = 2.2. BM = 4BM ( vì M là trung điểm BO )

=> BI + BJ = 4BM Thế vào (1) 

=> \(\frac{BA}{BF}+\frac{BC}{BE}=\frac{4BM}{BM}=4\)(2)

+) Kẻ BH // BG //FK  với H; G thuộc AC

Chứng minh tương tự như trên ta suy ra: \(\frac{BA}{AF}+\frac{AD}{AK}=4\)(3)

Cộng (2) + (3) vế theo vế:

\(\frac{BA}{BF}+\frac{BC}{BE}+\frac{BA}{AF}+\frac{AD}{AK}=8\)mà AD = BC

=> \(AB\left(\frac{1}{BF}+\frac{1}{AF}\right)+BC\left(\frac{1}{BE}+\frac{1}{AK}\right)=8\)(4)

Mặt khác: \(\frac{1}{BF}+\frac{1}{AF}=\frac{1^2}{BF}+\frac{1^2}{AF}\ge\frac{\left(1+1\right)^2}{BF+AF}=\frac{4}{AB}\) và \(\frac{1}{BE}+\frac{1}{AK}\ge\frac{4}{BE+AK}\)

KHi đó: \(8\ge AB.\frac{4}{AB}+BC.\frac{4}{BE+AK}\)

<=> \(BE+AK\ge BC\)

Dấu "=" xảy ra <=> BF = AF  và BE = AK 

Hay F là trung điểm AB.

+ Kẻ AH // FE // CI   \(\left(H,I\in BD\right)\)

+ \(\Delta AOH=\Delta COI\left(g.c.g\right)\)

\(\Rightarrow OH=OI\)

\(\Rightarrow BH+BI=BH+BO+OI\)

\(=BH+OH+BO=2BO=4BM\)

+ Xét \(\Delta ABH\)có : AH // FM theo định lí Ta - lét ta có : 

\(\frac{BA}{BF}=\frac{BH}{BM}\left(1\right)\)

+ Xét \(\Delta BCI\) có CI // ME theo định lí Ta - lét ta có : 

\(\frac{BC}{BE}=\frac{BI}{BM}\left(2\right)\)

+ Từ (1) và (2) \(\Rightarrow\)

\(\frac{BA}{BF}+\frac{BC}{BE}=\frac{BH}{BM}+\frac{BI}{BM}=\frac{BH+BI}{BM}=\frac{4BM}{BM}=4\)

Chúc bạn học tốt !!!

gfvfvfvfvfvfvfv555

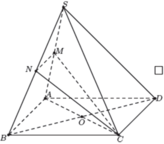
Đáp án B

Dễ thấy M N | | A B nên mặt phẳng (CMN) cắt mặt phẳng (ABCD) theo giao tuyến là đường thẳng qua C và song song với AB.

Vậy giao tuyến của (MNC) và (ABD) là đường thẳng CD.

Đề bài sai òi :v Vẽ hình ra đi bạn.

Giờ tui gán MN vô (SBD) thì giao tuyến của (SBD) và (SBC) là SB. Vậy nên SB phải song song với MN. Nhưng ko :) Song song chết liền hà :)

Đáp án D

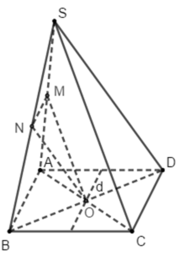
Theo câu 13, ta có MN // AB

Lại có: O ∈  (MNO) ∩  (ABCD)

Vậy giao tuyến của hai mặt phẳng (MNO) và (ABCD) là đường thẳng d đi qua O và song song với AB.

Qua S kẻ đường thẳng d song song AD (và BC)

Do \(\left\{{}\begin{matrix}S\in\left(SAD\right)\cap\left(SBC\right)\\AD||BC\\AD\in\left(SAD\right)\\BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow\) giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song AD, BC

\(\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)