d: \(x\left(x+1\right)\left(x^2+x+1\right)=42\left(1\right)\)

=>\(\left(x^2+x\right)\left(x^2+x+1\right)=42\)

Đặt \(a=x^2+x\)

Phương trình (1) sẽ trở thành \(a\left(a+1\right)=42\)

=>\(a^2+a-42=0\)

=>(a+7)(a-6)=0

=>\(\left(x^2+x+7\right)\left(x^2+x-6\right)=0\)

mà \(x^2+x+7=\left(x+\dfrac{1}{2}\right)^2+\dfrac{27}{4}>0\forall x\)

nên \(x^2+x-6=0\)

=>(x+3)(x-2)=0

=>\(\left[{}\begin{matrix}x+3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)

e: \(\left(x-1\right)\left(x-3\right)\left(x+5\right)\left(x+7\right)-297=0\left(2\right)\)

=>\(\left(x-1\right)\left(x+5\right)\left(x-3\right)\left(x+7\right)-297=0\)

=>\(\left(x^2+4x-5\right)\left(x^2+4x-21\right)-297=0\)

Đặt \(b=x^2+4x\)

Phương trình (2) sẽ trở thành \(\left(b-5\right)\left(b-21\right)-297=0\)

=>\(b^2-26b+105-297=0\)

=>\(b^2-26b-192=0\)

=>(b-32)(b+6)=0

=>\(\left(x^2+4x-32\right)\left(x^2+4x+6\right)=0\)

mà \(x^2+4x+6=\left(x+2\right)^2+2>0\forall x\)

nên \(x^2+4x-32=0\)

=>(x+8)(x-4)=0

=>\(\left[{}\begin{matrix}x+8=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=4\end{matrix}\right.\)

f: \(x^4-2x^2-144x-1295=0\)

=>\(x^4-7x^3+7x^3-49x^2+47x^2-329x+185x-1295=0\)

=>\(\left(x-7\right)\cdot\left(x^3+7x^2+47x+185\right)=0\)

=>\(\left(x-7\right)\left(x+5\right)\left(x^2+2x+37\right)=0\)

mà \(x^2+2x+37=\left(x+1\right)^2+36>0\forall x\)

nên (x-7)(x+5)=0

=>\(\left[{}\begin{matrix}x-7=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-5\end{matrix}\right.\)

\(\left(x-1\right)\left(x-3\right)\left(x+5\right)\left(x+7\right)=297\)

\(\Leftrightarrow\left[\left(x-1\right)\left(x+5\right)\right]\left[\left(x-3\right)\left(x+7\right)\right]=297\)

\(\Leftrightarrow\left(x^2+5x-x-5\right)\left(x^2+7x-3x-21\right)=297\)

\(\Leftrightarrow\left(x^2+4x-5\right)\left(x^2+4x-21\right)=297\) (*)

Đặt \(x^2+4x-13=y\)

Ta có phương trình (*) \(\Leftrightarrow\left(y+8\right)\left(y-8\right)=297\)

\(\Leftrightarrow y^2-64-297=0\)

\(\Leftrightarrow y^2-361=0\Leftrightarrow\left(y-19\right)\left(y+19\right)=0\)

\(\Leftrightarrow\left(x^2+4x-13-19\right)\left(x^2+4x-13+19\right)=0\)

\(\Leftrightarrow\left(x^2+4x-32\right)\left(x^2+4x+6\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x+8\right)\left(x^2+4x+6\right)=0\)

Ta có: \(x^2+4x+6=\left(x^2+4x+4\right)+2=\left(x+2\right)^2+2\)

Vì \(\left(x+2\right)^2\ge0\forall x\Rightarrow\left(x+2\right)^2+2\ge2>0\forall x\)

\(\Rightarrow\) Phương trình \(x^2+4x+6\) vô nghiệm.

Vậy \(\left(x-4\right)\left(x+8\right)\left(x^2+4x+6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-8\end{matrix}\right.\)

Vậy phương trình trên có tập nghiệm là S = {4:-8}

(x-1)(x-3)(x+5)(x+7)=297

⇔(x-1)((x+5)(x-3)(x+7)=297

⇔(x²+4x-5)(x²-4x-21)=297

Đặt x²+4x-13=t, ta được:

(t+8)(t-8)=297

⇔t²-64=297

⇔t²-64-297=0

⇔t²-361=0

⇔(t-19)(t+19)=0

\(\left\{{}\begin{matrix}t-19=0\\t+19=0\end{matrix}\right.< =>\left\{{}\begin{matrix}t=19\\t=-19\end{matrix}\right.\)

Với t=19, ta được:

x²+4x-13=19

⇔x²+4x-13-19=0

⇔x²+4x-32=0

⇔x²+8x-4x-32=0

⇔x(x+8)-4(x+8)=0

⇔(x+8)(x-4)=0

⇔\(\left\{{}\begin{matrix}x+8=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-8\\x=4\end{matrix}\right.\)

->phương trình có tập nghiệm là S=\(\left\{-8;4\right\}\)

Với t=-19,ta được:

x²+4x-13=-19

⇔x²+4x-13+19=0

⇔x²+4x+6=0

⇔x²+4x+4+2=0

⇔(x+2)²+2=0 (vì (x+2)²≥0 với ∀ ⇒(x+2)²+2 ≥ 2 >0)

->Phương trình vô nghiệm

Kết luận : Vậy phương trình có tập nghệm là S=\(\left\{-8;4\right\}\)

a, \(\left(x^2+x\right)^2+4\left(x^2+x\right)-12=0\)

\(\Leftrightarrow x^4+2x^3+x^2+4x^2+4x+12=0\)

\(\Leftrightarrow x^4+2x^3+5x^2+4x-12=0\)

\(\Leftrightarrow x^4-x^3+3x^3-3x^2+8x^2-8x+12x-12=0\)

\(\Leftrightarrow x^3\left(x-1\right)+3x^2\left(x-1\right)+8x\left(x-1\right)+12\left(x-1\right)=0\)

\(\Leftrightarrow\left(x^3+3x^2+8x+12\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left(x^3+2x^2+x^2+2x+6x+12\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[x^2\left(x+2\right)+x\left(x+2\right)+6\left(x+2\right)\right]\left(x-1\right)=0\)

\(\Leftrightarrow\left(x^2+x+6\right)\left(x+2\right)\left(x-1\right)=0\)

có : \(x^2+x+6>0\)

\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=1\end{cases}}}\)

b,  \(\left(x-1\right)\left(x-3\right)\left(x+5\right)\left(x+7\right)-297=0\)

\(\Leftrightarrow\left[\left(x-1\right)\left(x+5\right)\right]\left[\left(x-3\right)\left(x+7\right)\right]-297=0\)

\(\Leftrightarrow\left(x^2+4x-5\right)\left(x^2+7x-21\right)-297=0\)

đặt \(x^2+4x-13=t\)

\(\Leftrightarrow\left(t+8\right)\left(t-8\right)-297=0\)

\(\Leftrightarrow t^2-64-297=0\)

\(\Leftrightarrow t^2=361\)

\(\Leftrightarrow t=\pm19\)

có t rồi tìm x thôi

nhìn căng nhể :))

a) ( x - 1 )( x - 3 )( x + 5 )( x + 7 ) - 297 = 0

<=> [ ( x - 1 )( x + 5 ) ][ ( x - 3 )( x + 7 ) ] - 297 = 0

<=> ( x² + 4x - 5 )( x² + 4x - 21 ) - 297 = 0

Đặt t = x² + 4x - 5

pt <=> t( t - 16 ) - 297 = 0

<=> t² - 16t - 297 = 0

<=> t² - 27t + 11t - 297 = 0

<=> t( t - 27 ) + 11( t - 27 ) = 0

<=> ( t - 27 )( t + 11 ) = 0

<=> ( x² + 4x - 5 - 27 )( x² + 4x - 5 + 11 ) = 0

<=> ( x² + 4x - 32 )( x² + 4x + 6 ) = 0

<=> ( x² - 4x + 8x - 32 )( x² + 4x + 6 ) = 0

<=> [ x( x - 4 ) + 8( x - 4 ) ]( x² + 4x + 6 ) = 0

<=> ( x - 4 )( x + 8 )( x² + 4x + 6 ) = 0

Đến đây dễ rồi :)

bn lấy bài này ở đâu, làm sao lop8 giải dc, chị tui lop9 giai 

a) đặt t = x² +x 

t² +4t -12 =0

t² +4t +4 - 4 -12=0

(t+2 +4)( t +2-4) =0

t+6=0 => t =-6

t-2 =0 => t = 2

rui bn thay t = x²+x giải nhé

ai giải giùm milk vs\

câu này toán nâng cao lớp 8 mà . Bạn làm dc câu e , f  dc k làm dc làm jup milk vs ............ thanks

Nguyễn TrươngNguyễn Việt LâmNguyenTruong Viet TruongKhôi BùiAkai HarumaÁnh LêDƯƠNG PHAN KHÁNH DƯƠNGPhùng Tuệ Minhsaint suppapong udomkaewkanjana

Unruly KidAkai HarumaNguyễn Thanh HằngLê Anh DuyKhôi BùiNguyễn Việt LâmNguyễn TrươngDũng NguyễnNguyenTRẦN MINH HOÀNG

Bài `1:`

`h)(3/4x-1)(5/3x+2)=0`

`=>[(3/4x-1=0),(5/3x+2=0):}=>[(x=4/3),(x=-6/5):}`

______________

Bài `2:`

`b)3x-15=2x(x-5)`

`<=>3(x-5)-2x(x-5)=0`

`<=>(x-5)(3-2x)=0<=>[(x=5),(x=3/2):}`

`d)x(x+6)-7x-42=0`

`<=>x(x+6)-7(x+6)=0`

`<=>(x+6)(x-7)=0<=>[(x=-6),(x=7):}`

`f)x^3-2x^2-(x-2)=0`

`<=>x^2(x-2)-(x-2)=0`

`<=>(x-2)(x^2-1)=0<=>[(x=2),(x^2=1<=>x=+-2):}`

`h)(3x-1)(6x+1)=(x+7)(3x-1)`

`<=>18x^2+3x-6x-1=3x^2-x+21x-7`

`<=>15x^2-23x+6=0<=>15x^2-5x-18x+6=0`

`<=>(3x-1)(5x-1)=0<=>[(x=1/3),(x=1/5):}`

`j)(2x-5)^2-(x+2)^2=0`

`<=>(2x-5-x-2)(2x-5+x+2)=0`

`<=>(x-7)(3x-3)=0<=>[(x=7),(x=1):}`

`w)x^2-x-12=0`

`<=>x^2-4x+3x-12=0`

`<=>(x-4)(x+3)=0<=>[(x=4),(x=-3):}`

`m)(1-x)(5x+3)=(3x-7)(x-1)`

`<=>(1-x)(5x+3)+(1-x)(3x-7)=0`

`<=>(1-x)(5x+3+3x-7)=0`

`<=>(1-x)(8x-4)=0<=>[(x=1),(x=1/2):}`

`p)(2x-1)^2-4=0`

`<=>(2x-1-2)(2x-1+2)=0`

`<=>(2x-3)(2x+1)=0<=>[(x=3/2),(x=-1/2):}`

`r)(2x-1)^2=49`

`<=>(2x-1-7)(2x-1+7)=0`

`<=>(2x-8)(2x+6)=0<=>[(x=4),(x=-3):}`

`t)(5x-3)^2-(4x-7)^2=0`

`<=>(5x-3-4x+7)(5x-3+4x-7)=0`

`<=>(x+4)(9x-10)=0<=>[(x=-4),(x=10/9):}`

`u)x^2-10x+16=0`

`<=>x^2-8x-2x+16=0`

`<=>(x-2)(x-8)=0<=>[(x=2),(x=8):}`

(x – 1)(x – 3)(x + 5)(x + 7) = 0

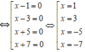
Vậy tập nghiệm của phương trình là S = { -7;-5;1;3}

\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)

\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)

\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)

\(\Leftrightarrow x^2-9-x^2+3x=0\)

\(\Leftrightarrow3x-9=0\)

\(\Leftrightarrow3x=9\)

\(\Leftrightarrow x=3\left(n\right)\)

Vậy \(S=\left\{3\right\}\)

\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)

\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)

\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)

\(\Leftrightarrow12x-9-12x+20+2x-7>0\)

\(\Leftrightarrow2x+4>0\)

\(\Leftrightarrow2x>-4\)

\(\Leftrightarrow x>-2\)