Cho hình vẽ, a // b. Kẻ pgiác Mt của M1, Nk của N1.Chứng tỏ Mt // Nk. M 1 1 N a b
Đọc tiếp
Cho hình vẽ, a // b. Kẻ pgiác Mt của M1, Nk của N1.Chứng tỏ Mt // Nk.
Những câu hỏi liên quan
cho hình vẽ,biết góc M1 và N1=125 độ,Q1=75 độ
a,vẽ hình ,ghi gt-kl
b chứng minh x//y
c tính m2,p1,p2
d, kẻ tia phân giác mt của pmn cắt tia phân giác nz của mnq tại k.tính số đo mkn
Cho tam giác MNP nhọn nội tiếp (O) có MN < MP. Vẽ các đường cao MH, NK, PQ, đường kính MT. Chứng minh a) MN.MP=MH.MT b) Tứ giác NQKP nội tiếp c) MT vuông góc với KQ (Bạn nào rảnh giúp mình giải với 😭😭 mình đang cần gấp lắm ạ!!!)
Xét $\Delta MNH$ và $\Delta P$ ta có:
$\large \widehat{MHN}=\widehat{MPT}=90^o$
$\large \widehat{MNP}=\widehat{MTP}$(Hai góc cùng chắn cung $MP$)
Do đó $\large \Delta MNH \sim \Delta MTP$ $(g-g)$
Từ đó: $\frac{MN}{MT}=\frac{MH}{MP}\Leftrightarrow MN.MP=MH.MT$
Xét tứ giác $NQKP$ ta có:
$\large \widehat{NQP}=\widehat{PKN}=90^o$
Mà hai góc này cùng chắn cung $NP$
Do đó tứ giác $NQKP$ là tứ giác nội tiếp
Suy ra: $\large \widehat{PKQ}+\widehat{PNQ}=180^o$ (Hai góc nội tiếp đối nhau)
Đồng thời ta có $\large \widehat{PKQ}+\widehat{MKQ}=180^o\Rightarrow \widehat{MNP}=\widehat{MTP}=\widehat{MKQ}$
Gọi $A$ là giao điểm của $QK$ và $MT$
Xét tứ giác $TPKA$ ta có:
$\large \widehat{MTP}+\widehat{PKQ}=\widehat{PKQ}+\widehat{MKQ}=180^o$
Mà hai góc này ở vị trí đối nhau nên tứ giác $TPAK$ là tứ giác nội tiếp
$\large \Leftrightarrow \widehat{MPT}+\widehat{TAK}=180^o\Leftrightarrow \widehat{TAK}=180^o-\widehat{MPT}=90^o$
Do đó $MT$ vuông góc với $QK$
Hình:
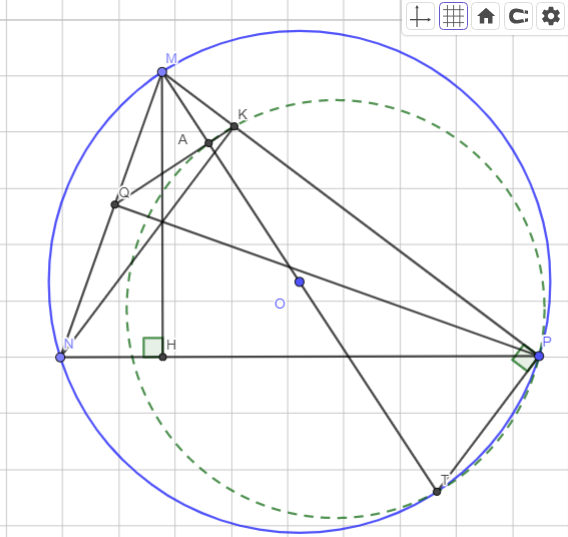
Đúng 1
Bình luận (2)
Cho ΔABC có M là trung điểm của BC , AM vuông góc với BC . Từ M kẻ Mt // AC , từ B kể đường vuông góc với BC cắt Mt tại N .
a, Chứng minh AM là phân giác của góc BAC ,
b, Chứng minh ΔAMB = ΔNBM,
c, MN cắt AB tại I . Chứng minh I là trung điểm của AB ,
d, Chứng minh AN // BC .
cho tam giác ABC cân ở A . trên cạnh BC lấy M,N sao cho BM=CN ( M nằm giữa Bvà N
a) chứng minh tam giác AMN cân
b) gọi D là trung điểm của MN chứng minh AD là phân giác của góc BAC
c) Kẻ MH vuông góc với AB , NK vuông góc với AC chứng minh MH = NK
d) chứng minh MH ,AD , NK đồng quy
Cho hai đường thẳng m'm , n'n , đường thẳng xy cắt hai đoạn thẳng tại M và N có góc mMN = góc n'NM . Kẻ hai tia phân giác Mt , Nz của góc mMN và n'NM . chứng tỏ Mt // Nz
cho tam giác ABC vuông tại A. M là trung điểm của BC. trên tia đối của MA lấy D sao cho M là trung điểm của AD.
Từ M kẻ MK vuông góc với AC tại K, kẻ MN vuông góc với Ab tại N, điểm E là gạo điểm của AM và NK. chứng minh ME =1/2 NK.
Bài 1 : Tìm 3 số nguyên a,b,c thỏa mãn : a+b=-4 ; b+c=-6 ; c+a=12
Bài 2 Cho đoạn thẳng MN=2a. K là điểm nằm giữa M,N. Gọi A là trung điểm của đoạn MK, B là trung điểm của đoạn NK. Chứng tỏ AB=a?
Từ một điểm M bên ngoài đường tròn (O) kẻ tiếp tuyến MT và cát tuyến MAb. Vẽ đường tròn (O') ngoại tiếp tam giác MAT. Từ M vẽ tiếp tuyến xy của đường tròn (O').Chứng minh rằng:
a, MT2=MA.MB
b, BT//xy
Bài 1 :Cho tam giác ABC cân ( AB=AC) , D thuộc AB ; E thuộc AC. M là trung điểm của BC . C/m : a)DE song song với BC
b) Tam giác MBD = Tam giác MCE ( Đã vẽ đc hình rồi )
Bài 2 :Cho tam giác ABC ;M.N thuộc BC sao cho BM = CN; Từ M,N kẻ MH;NK song song với AB ( H,K thuộc AC )
C/M:MH+NK=AB(Đã vẽ đc hình)