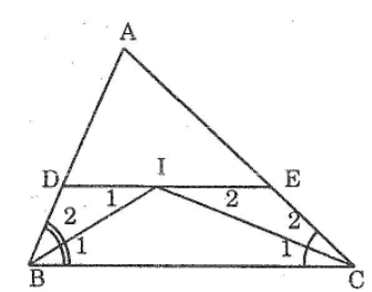
CHO TAM GIÁC ABC CÁC IA PHÂN GIÁC CỦA B VÀ C CẮT NHAU Ở I QUA I KẺ ĐT' SONG SONG VS BC CẮT AB Ở D CẮT AC Ở E CHỨNG MINH RẰNG DE=BD+CE

Những câu hỏi liên quan
CHO TAM GIÁC ABC CÁC TIA PHÂN GIÁC CỦA B VÀ C CẮT NHAU Ở I QUA I KẺ ĐT' SONG SONG VS BC CẮT AB Ở D CẮT AC Ở E . CHỨNG MINH RẰNG DE=BD+CE
Cho tam giác ABC , các tia phân giác của góc B và C cắt nhau ở I . Qua I kẻ đường thẳng song song BC cắt AB ở D , cắt AC ở E Chứng minh :DE=BD+CE
\(\widehat{I_1}=\widehat{B_2}\)(2 góc slt của DE // BC) mà\(\widehat{B_1}=\widehat{B_2}\)(BI là phân giác góc ABC)\(\Rightarrow\widehat{I_1}=\widehat{B_1}\Rightarrow\Delta BDI\)cân tại D => BD = DI
\(\widehat{I_2}=\widehat{C_2}\)(2 góc slt của DE // BC) mà\(\widehat{C_1}=\widehat{C_2}\)(CI là phân giác góc ACB)\(\Rightarrow\widehat{I_2}=\widehat{C_1}\Rightarrow\Delta IEC\)cân tại E => IE = EC
Vậy DE = DI + IE = BD + CE (đpcm)
Đúng 2
Bình luận (0)
Vì DE song song với BC => \(\widehat{DIB}=\widehat{IBC}\) ( SLT) . Mà \(\widehat{IBC}=\widehat{DBI}\) ( BI là p/g của \(\widehat{ABC}\) ) => \(\widehat{DIB}=\widehat{DBI}\) theo định lý => tam giác DIB cân tại D => DB = DI
Vì DE song song với BC => \(\widehat{EIC}=\widehat{ICB}\)( SLT) .Mà \(\widehat{ECI}=\widehat{ICB}\) ( CI là p/g của \(\widehat{ECB}\) ) => \(\widehat{EIC}=\widehat{ECI}\) .Theo định lý => tam giác IEC cân tại E => EI = EC
Vì DE = DI + IE . Mà DI = DB ; IE = EC => DE = DB + CE
Vậy DE = DB + CE
Đúng 2
Bình luận (0)
Kẻ CI giao AB tại H, BI giao AC tại K
Ta có góc HIB = IBC + ICB (góc ngoài tam giác), DE // BC => HID = ICB
=> DIB = IBC mà BI là phân giác nên DBI = IBC => DIB = DBI => tam giác BDI cân tại D => DB = DI
Tương tự, ta có góc KIC = IBC + ICB (góc ngoài tam giác), DE // BC => KIE = IBC
=> EIC = ICB mà CI là phân giác nên ECI = ICB => EIC = ECI => tam giác CEI cân tại E => CE = EI
Ta có: DE = DI + IE mà DI = DB, IE = CE => DE = DB + CE => chứng minh được DE = BD + CE
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ Đường tẳng song song với BC cắt AB ở D và cắt AC ở E. Chứng minh DE = BD + CE
Cho tam giác ABC , các tia phân giác của góc B và C cắt nhau ở I . qua I kẻ ddường thẳng song song BC cắt AB ở D , cắt AC ở E .
chứng minh : DE=BD+CE
Bài 6: Cho tam giác ABC các tia phân giác góc B, góc C cắt nhau tại I, qua I kẻ đường thẳng song song vố BC cắt AB ở D và cắt AC ở E
a) Chứng minh: tam giác BDI là tam giác cân.
b) Chứng minh: DE=BD+CE
a: Xét ΔBDI có \(\widehat{DIB}=\widehat{DBI}\left(=\widehat{IBC}\right)\)
nên ΔBDI cân tại D
b: Xét ΔEIC có \(\widehat{EIC}=\widehat{ECI}\)
nên ΔEIC cân tại E
Ta có: DE=DI+IE
nên DE=BD+EC
Đúng 2
Bình luận (1)
Cho tam giác ABC . Các tia phân giác của góc ABC và góc ACB cắt nhau ở I . Qua I kẻ đường song song với BC cắt AB tại D và cắt AC tại E . Chứng minh DE=BD+CE
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB, AC theo thứ tự là D,E.
Chứng minh rằng: DE = BD + CE
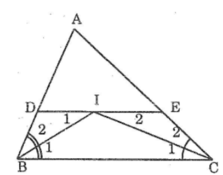
Ta có: DI // BC (giả thiết)
Suy ra:∠I1 =∠B1(so le trong) (1)
Lại có:∠B1 =∠B2 (2)
(vì BI là tia phân giác góc ABC)
Từ (1) và (2) suy ra:∠I1 =∠B2
=>∆BDI cân tại D =>BD=DI (3)
Mà IE // BC (gt) => ∠I2 =∠C1 (so le trong) (4)
Đồng thời: ∠C1=∠C2 (vì CI là phân giác của góc ACB) (5)
Từ (4) và (5) suy ra: ∠I2=∠C2. Suy ra ∠CEI cân tại E
Suy ra: CE = EI (6)
Từ (3) và (6) suy ra: BD + CE = DI + EI = DE
Đúng 0
Bình luận (0)
Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC, gọi giao điểm của đường thẳng này với AB, AC theo thứ tự là D, E. Chứng minh rằng DE=BD+CE.
tôi còn đang phải đi hỏi đây đồ điên
Đúng 0
Bình luận (0)
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB, AC theo thứ tự D, E. Chứng minh rằng DE = BD + CE
Ta có hình vẽ:
Ta có: BI là pg góc B
=> góc DBI = góc IBC
Mà góc DIB = góc IBC (DE // BC)
=> góc DBI = góc DIB
=> tam giác BDI cân
=> BD = DI
Ta có: CI là phân giác góc C
=> góc ECI = góc ICB
Mà góc EIC = góc ICB (DE // BC)
=> góc ECI = góc EIC
=> tam giác CEI cân
=> CE = IE
Ta có: BD = DI; CE = IE
=> BD + CE = DI + IE
hay BD + CE = DE
hay DE = BD + CE
Đúng 1
Bình luận (0)
Ta có: DI // BC (gt)
Suy ra:∠I1 =∠B1(so le trong) (1)
Lại có:∠B1 =∠B2 (2)
(vì BI là yia phân giác góc B)
Từ (1) và (2) suy ra:∠I1 =∠B2
=>∆BDI cân tại D =>BD=DI (3)
Mà IE // BC (gt) =>∠I1 =∠C1 (so le trong) (4)
Đồng thời: ∠C1=∠C2 (vì CI là phân giác của góc C) (5)
Từ (4) và (5) suy ra: ∠C1=∠C2. Suy ra. ∠CEI cân tại E
Suy ra: CE = EI (hai cạnh tương ứng) (6)
Từ (3) và (6) suy ra: BD + CE = DI + EI = DE
Đúng 1
Bình luận (0)