Cho \(\Delta\)ABC vuông cân tại A , trung tuyến AM , E \(\in\) BC ; BH vuông góc với AE , CK vuông góc với AE .
Chứng minh \(\Delta\)MHK vuông cân !
Cho \(_{\Delta ABC}\)vuông cân tại A , trung tuyến AM . E \(\in\)BC, BH , CK \(\perp\)AE, ( H,K\(\in\)AE) . Chứng minh \(\Delta MHK\)vuông cân
Cho \(\Delta\)ABC vuông cân tại A , trung tuyến AM . E thuộc BC , BH vuông với AE , CK vuông với AE (H,K thuộc AE). Chứng minh tam giác MNK vuông cân
Cho \(\Delta ABC\) vuông cân tại A. Kẻ AM là trung tuyến của \(\Delta ABC\). Điểm E thuộc cạnh BC. BH vuông góc với AE, CK vuông góc với AE. (CHỉ cần vẽ hình)
Bài 17: Cho tam giác ABC cân tại A. Gọi M là trung điểm BC.
a, Chứng minh \(\Delta\) ABM =\(\Delta\) ACM
b, Chứng minh AM là phân giác góc BAC và AM vuông góc BC.
c, Lấy E bất kì trên đoạn AM. Chứng minh tam giác EBC cân.
Lời giải:
a.
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.
Cho tam giác ABC vuông cân tại A, trung tuyến AM. Lấy điểm E thuộc BC. Kẻ BH,CK vuông góc với AE.CMR:Tam giác MHK vuông cân
. Cho tam giác ABC vuông cân tại A, trung tuyến AM. Lấy E \(\in\) BC. BH, CK AE (H, K \(\in\) AE). Chứng minh rằng tam giác MHK vuông cân.
cho tam giác ABC vuông cân tại A trung tuyến AM E thuộc BC , BH vuông với AE , CK vuông với AE
cm tam giác MHK CÂN
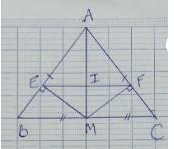
Cho tam giác ABc cân tại A đường trung tuyến AM ( M thuộc BC)
a, C/ m tam giác ABM =ACM
Từ M kẻ ME vuông góc AB tại E kẻ MF vuông góc vs AC tại F
C/m AM trung trực È
a) Xét ΔABM và ΔACM có:
AB = AC (ΔABC cân tại A)
Cạnh AM chung
BM = CM (AM là đường trung tuyến của BC)
⇒ ΔABM = ΔACM (c.c.c)
Vậy ΔABM = ΔACM
Bài 1:
1. Cho \(\Delta\)ABC vuông tại A. Có AB bằng \(\frac{1}{2}\)BC. Tính góc C?
2. Cho \(\Delta\)ABC vuông tại A. Có góc B=30 độ. C/m AC=\(\frac{1}{2}\)BC
3. Cho \(\Delta\)ABC. Có trung tuyến BM=CN. C/m \(\Delta\)ABC cân tại A.
4. Cho \(\Delta\)ABC có trung tuyến AM đồng thời là đường phân giác góc A. C/m \(\Delta\)ABC cân tại A.
Giúp mk nhé mai phải nộp rùi!!!
Bài 1:
Gọi M là trung điểm của BC
Vẽ BE là tia phân giác của góc B, E thuộc AC
nối M với E
ta có: BM =CM = 1/2.BC ( tính chất trung điểm)
AB=1/2.BC (gt)
=> BM = CM= AB ( =1/2.BC)
Xét tam giác ABE và tam giác MBE
có: AB = MB (chứng minh trên)
góc ABE = góc MBE (gt)
BE là cạnh chung
\(\Rightarrow\Delta ABE=\Delta MBE\left(c-g-c\right)\)
=> góc BAE = góc BME = 90 độ ( 2 cạnh tương ứng)
=> góc BME = 90 độ
\(\Rightarrow BC\perp AM⋮M\)
Xét tam giác BEM vuông tại M và tam giác CEM vuông tại M
có: BM=CM(gt)
EM là cạnh chung
\(\Rightarrow\Delta BEM=\Delta CEM\left(cgv-cgv\right)\)
=> góc EBM = góc ECM ( 2 cạnh tương ứng)
mà góc EBM = góc ABE = 1/2. góc B (gt)
=> góc EBM = góc ABE = góc ECM
Xét tam giác ABC vuông tại A
có: \(\widehat{B}+\widehat{ECM}=90^0\) ( 2 góc phụ nhau)
=> góc EBM + góc ABE + góc ECM = 90 độ
=> góc ECM + góc ECM + góc ECM = 90 độ
=> 3.góc ECM = 90 độ
góc ECM = 90 độ : 3
góc ECM = 30 độ
=> góc C = 30 độ
cho tam giác ABC vuông cân tại A , trung tuyến AM . E thuộc BC , BH vuông góc AE , CK vuông góc AE , (H,K thuộc AE) . CM :Tam giác MHK vuông cân