a)Vì E đối xứng với điểm M qua điểm D nên M,D,E thẳng hàng và DM = DE (1)

Áp dụng tính chất đường trung bình cho DBAC ta có DM//AC.

Mà DABC vuông tại A nên CA ^ AB Þ MD ^ AB (2)

Từ (1) và (2) Þ E đối xứng với M qua đường thẳng AB.

b) Tứ giác AEMC là hình bình hành, tứ giác AEBM là hình thoi.

c) Chu vi tứ giác AEBM là 4BM = 8 (cm)

d) nếu tứ giác AEBM là hình vuông thì ME = AB mà ME = AC (do ACME là hình bình hành) Þ AC = AB Þ DABC vuông cân tại A.

A) Xét tam giác MDA và tam giác EDB có :
MD=DE( GT)

DA=DB( GT)

góc EDB=góc MDA ( góc đối đỉnh)

vậy tam giác MDA = tam giác EDB( C-G-C)

suy ra : DE=MA( hai canh tương ứng)

 chứng minh tương tự ta lại có : tam giác MDB= tam giác EDA 

suy ra : MB=AE( hai canh tương ứng)

mà ta lại có AM là đường trung tuyến ứng với cạnh huyền vậy AM=1/2BC=MB

vậy : MA=MB=AE=BE

suy ra : tứ giác AEBM là hình thoy

B) Xét tứ giác CMEA có :

MB song song với AE và bằng MB =AE ( theo phần a)

mà ta lại có : MC = MB

vậy AE song song với MC

AE=MC( chứng minh trên)

vậy tứ giác CMEA là HBH

 Mà I lại là trung điểm của đường chéo AM 

vậy I cũng là trung điểm của đường chéo CE

suy ra :  C,i.E thẳng hàng

C) tam giác ABC phải là tam giác vuông cân thì tứ giác AEBM mới là hình vuông 

 bở lẽ khi tam tam giác ABC vuuong cân thì ta sẽ có góc CBA = 45 độ

mà BA lại là đường phân giác của góc MBE ( theo phần a  tứ giác AEMB là hình thoi)

 nên góc MBE =45*2=90độ

mà phần a ta lại có  tứ giác AMBE là hình thoi 

vậy tứ giác AMBE là hình vuông

mình làm xong rồi nhớ mình nhé mình cảm ơn ^_^

câu a) bn ấy lm hơi dài nên mk có cách khác

c/m EBMA là hbh (2 đường chéo cắt tại trung điểm mỗi đường)

mà có AB vuông góc EM (t/c đối xứng)

vậy AEBM là hình thoi

 a) Ăn cắp vàng ở Hà Tây 

b) Ăn trộm vàng ở Hà Tây 

c) Ăn cướp vàng ở Hà Tây

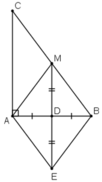
a) Ta có MB = MC, DB = DA

⇒ MD là đường trung bình của ΔABC

⇒ MD // AC

Mà AC ⊥ AB

⇒ MD ⊥ AB.

Mà D là trung điểm ME

⇒ AB là đường trung trực của ME

⇒ E đối xứng với M qua AB.

b) + MD là đường trung bình của ΔABC

⇒ AC = 2MD.

E đối xứng với M qua D

⇒ D là trung điểm EM

⇒ EM = 2.MD

⇒ AC = EM.

Lại có AC // EM

⇒ Tứ giác AEMC là hình bình hành.

+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.

Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.

c) Ta có: BC = 4cm ⇒ BM = 2cm

Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm

d)- Cách 1:

Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC

Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.

- Cách 2:

Hình thoi AEBM là hình vuông ⇔ AM ⊥ BM

⇔ ΔABC có trung tuyến AM là đường cao

⇔ ΔABC cân tại A.

Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.

a) Ta có: MB = MC (giả thiết)

DA = DB (Giả thiết)

⇒ DM là đường trung bình của Δ ABC

⇒ DM//AC

Mặt khác ABC vuông tại A

⇒ AC ⊥ AB ⇒ DM ⊥ AB ⇒ DE ⊥ AB (*)

E là điểm đối xứng với M qua D ⇒ DM = DE (**)

Từ (*) và (**) ta suy ra: Điểm E đối xứng với M qua AB

b) Ta có AB ⊥ EM và DE = DM, DA = DB

⇒ Tứ giác AEBM là hình thoi

⇒ AE//BM mà BM = MC ⇒ AE//MC và AE = MC

⇒ tứ giác AEMC là hình bình hàng

c) Ta có BC = 4 (cm) ⇒ BM = BC/2 = 2(cm)

Chu vi hình thoi ABEM là P = 4BM = 8 (cm)

d) Hình thoi AEBM là hình vuông khi góc ∠AMB = 900

⇒ AM ⊥ BC

Mặt khác: AM là trung tuyến của tam giác vuông ABC

Suy ra: Δ ABC vuông cân tại A

Điều kiện: Δ ABC vuông cân tại A

 a) Ta có: E và M đối xứng với nhau qua D 
=> DE = DM ; ME vuông góc AB 
Ta có BD = DA ( D là trun điểm AB ) 
mà ME vuông góc AB ( cmt ) 
=> AB là trung trực của ME hay E và M đối xứng nhau qua D 
b) Xét Tam giác ABC có: 
M là trung điểm BC ( gt ) 
D là trung điểm AB ( gt) 
=> DM là đường trung bình tam giác ABC 
=> DM // AC; DM = 1/2AC 
mà E thuộc DM 
nên EM // AC 
Xét tứ giác AEMC có: 
EM // AC ( cmt) 
EM = AC ( cùng = 2DM ) 
=> Tứ giác AEMC là hình bình hành( tứ giác có 2 cạnh đối vừa // vừa = nhau là hình bình hành) 
c) Xét tứ giác AEBM có: 
ED = DM ( gt ) 
DB = AD ( gt ) 
=> Tứ giác AEBM là hình bình hành ( D/h 5 ) 
mà AB vuông góc EM 
=> hbh AEBM là hình thoi ( D/h 3 ) 
d) Ta có : AM = 1/2BC ( trung tuyến ứng với cạnh huyền) 
=> AM = 1/2 . BC = 1/2. 5 = 2,5 (cm) 
Chu vi hình thoi AEBM: 
2,5 . 4 =10 (cm) 
e) Nếu AEBM là hình vuông 
thì Â= Ê= góc B= góc M= 90 độ 
=>AM vuông góc BC 
=> AM vừa là đường trung tuyến vừa là đường cao tam giác ABC 
=> Tam giác ABC vuông cân tại A 
Vậy tam giác ABC vuông cân ở A thì AEBM là hình vuông

Mấy bạn giúp mình với, mình gấp lắm ạ =(((