trên tia Ax lấy 2 điểm E;F sao cho : AE=3,5 , AF=7
a) trong 3 điểm A:Ế:F điểm nào nằm giữa
b) tinh EF
c) điểm E có là trung điểm đoạn thẳng AF không?
Cho 2 tia Ax và Ay đối nhau. Trên tia Ax lấy điểm E , tia Ay lấy điểm D. Sao cho AE =2cm, AD=3cm
A) trong 3 điểm A,E,D điểm nào nằm giữa 2 điểm còn lại?
B) tính AB
Cho góc xAy. Lấy điểm B trên tia Ax điểm D trên tia Ay sao cho AB= AD . Trên tia Bx lấy điểm E trên tia Dy lấy điểm C sao cho BE = DC. Chứng minh rằng 2 tam giác ABC và ADE bằng nhau.
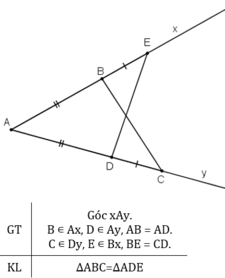
Ta có: AB = AD, BE = DC ⇒ AB + BE = AD + DC hay AE = AC.
Xét ΔABC và Δ ADE có:
AC = AE (cmt)
Góc A chung
AB = AD (gt)
⇒ ΔABC = ΔADE (c.g.c)
cho góc xAy<180 độ trên tia Ax lấy 2 điểm D và E trên tia Ay lấy 2 điểm D' và E' sao cho AD=AD' ; AE=AE' . CMR: DE'=D'E
Cho góc xAy, trên tia Ax lấy điểm D và E, trên tia Ay lấy 2 điểm F và G sao cho FD//EG. Đường thẳng kẻ qua G//FE cắt tia Ax ở H. Chứng minh: AE2 =AD.AH
FD//EG
Áp dụng định lý Ta let ta có:
\(\frac{AD}{AE}=\frac{AF}{AG}\) (1)
FE // GH
Áp dụng định lý Ta lét ta có:
\(\frac{AE}{AH}=\frac{AF}{AG}\) (2)
Từ (1) và (2) => \(\frac{AD}{AE}=\frac{AE}{AH}\)
=> AE²=AD.AH (đpcm)
Nguồn: nttxyhthkbgd1
cho đoạn thẳng AB có O là trung điểm trên 2 nửa mặt phẳng đối nhau bờ AB, vẽ các tia Ax và By cùng vuông góc với ab
trên tia Ax lấy điểm C trên tia By lấy điểm D sao cho AC=BD
a) chứng mih rằng O là trung điểm của CD
b) trên cạnh BC lấy điểm E, trên cạnh BC lấy điểm F, sao cho BE = AF chứng minh O là trung điểm của EF
giúp với mai phải nộp rồi ko nộp là bị ăn tát đấy :(
pls giúp mình với mang ơn mấy bạn nhiều!!!!
thanks
Cho đoạn thẳng AB và trung điểm O của đoạn thẳng đó . Trên 2 nửa mặt phẳng đối nhau bờ AB , kẻ 2 tia Ax và BY sao cho Ax // By . Trên tia Ax lấy 2 điểm C và E ( E nằm giữa A và C ) , trên tia By lấy 2 điểm B và F sao cho BD = AC , BF = AE . Chứng minh rằng :
a ) Ba điểm C , O , D thẳng hàng và 3 điểm E , O , F thẳng hàng
b ) DE = CF và DE // CF
Cho đoạn thẳng AB và trung điểm O của đoạn thẳng đó . Trên 2 nửa mặt phẳng đối nhau bờ AB , kẻ 2 tia Ax và BY sao cho Ax // By . Trên tia Ax lấy 2 điểm C và E ( E nằm giữa A và C ) , trên tia By lấy 2 điểm B và F sao cho BD = AC , BF = AE . Chứng minh rằng :
a ) Bà điểm C , O , D thẳng hàng và 3 điểm E , O , F thẳng hàng
b ) DE = CF và DE // CF
Vì Ax//By;C,E thuộc Ax;D,F thuộc By=>Ac//BD, AE//BF
=>góc CAO=góc OBD
Góc AEO=góc OFD
Góc ACO= góc ODB
xét tam giác ACO và tam giác OBD ta có
OA=OB;Góc CAO=BOD;ACO=ODB
=>hai tam giác này bằng nhau
=>góc COA=BOD(2 góc tương ứng )
Mà A,O,B thửng hàng=>góc COB+COA=180 độ
=>góc BOD+COB=180 độ
=>O,C,D thẳng hàng
tương tự chứng minh với E,O,F
b,Từ những tam giác bằng nhau ta có được OE=OF;CO=OD
xét tam giác OED và OCF có OE=OF; CO=OD; góc COF=EOD( 2 góc đối đỉnh)
=>góc FOD=CDE; DE=CF(2 cạnh tương ứng)
mà hai góc này ở vị trí so le trong của hai đoạn thẳng DE và CF được cắt bởi đoạn DC
=>DE//CF
má ơi trình bày trên máy tính khó qua cơ. gấp 3 lần thời gian trình bày ở vở luôn
ý:(((
(
thế nên em rút gọn phần chứng minh tương tự. dễ hiểu mà. cố tìm hiểu nha. không khó lắm đau. học mà tự mình tìm ra được vui lắm, còn nắm dược kiến thức nữa. thông cảm em không có thời gian trình bày hết:))))))))))))
trên tia Ax lấy hai điểm B và C sao cho AB=45cm, AC=9cm a) chứng tỏ B là trung điểm của đoạn thẳng AC
b) trên tia đối của tia Ax lấy điểm I sao cho a là trung điểm của IB. tính IC
c) trên tia đối của tia CA lấy điểm E ( E khác C).hãy so sánh EB với trung bình cộng của hai đoạn thẳng
giúp mik vs mik cần gấp ak.Xin c.ơn!🐰
Vẽ về một phía của đoạn thẳng AB=10 cm các tia Ax, By vuông góc với AB. Trên tia Ax lấy điểm D sao cho AD=10 cm. Trên tia By lấy điểm E sao cho BE=2 cm Trên đoạn thẳng AB lấy điểm C sao cho AC=4cm. D C E ^ có là góc vuông hay không
Bài 2. Cho góc xAy. Lấy điểm B trên Ax, điểm D trên Ay sao cho AB = AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE = DC. Chứng minh AABC = AADE
Bài 3. Cho góc nhọn xOy và tia Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Lấy điểm I thuộc tia Oz Chứng minh rằng a) AAOI = ABOI b) AB 1 OI
Bài 4. Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC a) Chứng minh ABAC = ABAD b) Trên tia đối của tia AB lấy điểm M. Chứng minh AMBD = AMBC
Bài 4:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
BA chung
AC=AD
Do đó: ΔABC=ΔABD
b: Xét ΔMAC vuông tại A và ΔMAD vuông tại A có
MA chung
AC=AD
Do đó: ΔMAC=ΔMAD
Xét ΔMBD và ΔMBC có
MB chung
BD=BC
MD=MC
Do đó: ΔMBD=ΔMBC