Chứng minh từ đẳng thức ad=bc(c,d khác 0) ta có thể suy ra tỉ lệ thức sau a/c=b/d

Những câu hỏi liên quan
Chứng minh rằng từ đẳng thức ad=bc (c, d khác 0 ) ta có thể suy ra được tỉ lệ thức a : c = b : d
\(ad=bc=>ad:dc=bc:dc=>\frac{ad}{dc}=\frac{bc}{dc}=>\frac{a}{c}=\frac{b}{d}\)
Đúng 0
Bình luận (0)
\(ad=bc\Rightarrow\frac{ad}{cd}=\frac{bc}{cd}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Đúng 0
Bình luận (0)
Chứng minh rằng từ đẳng thức ad=bc (c,d khác 0 ) ta có thể suy ra được tỉ lệ thức a/c=c/d
\(\frac{a}{b}=\frac{c}{d}\) chứ bạn
Đúng 0
Bình luận (0)
Chứng minh rằng từ đẳng thức ad=bc (c,d khác 0), ta có thể suy ra được tỉ lệ thức: \(\frac{a}{c}=\frac{b}{d}\)
\(ad=bc\Rightarrow ad:dc=bc:dc\Rightarrow\frac{ad}{dc}=\frac{bc}{dc}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Đúng 0
Bình luận (0)
ad=bc => ad:dc=bc:dc => ad/dc=bc/dc=> a/c=b/d
đúng ko?????
Đúng 0
Bình luận (0)
chứng minh rằng từ đẳng thức ad = bc (c,d /0)ta có thể suy ra được tỉ lệ thức a/c .b/d
Xem chi tiết
ad=bc
=>ad/cd=bc/cd(vì cd#0)
=>a/c=b/d (₫pcm)
k mk nha
Đúng 0
Bình luận (0)
Chứng minh rằng từ đẳng thức ad = bc (c, d ≠ 0), ta có thể suy ra được tỉ lệ a c = b d
Ta có: ad = bc; c ≠ 0; d ≠ 0 suy ra cd ≠ 0
Chia cả 2 vế cho cd. Suy ra:
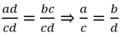
Đúng 0
Bình luận (0)
Chứng minh rằng từ đẳng thức ad=bc (c, d\(\ne\)0), ta có thể suy ra được tỉ lệ thức a/c=b/d
\(ad=bc=>ad:dc=bc:dc=>\frac{ad}{dc}=\frac{bc}{dc}=>\frac{a}{c}=\frac{b}{d}\)
Đúng 0
Bình luận (0)
nếu a/c=b/d thì a.d/cd=bc/cd=>ad=bcthí a/c=b/d
Đúng 0
Bình luận (0)
\(ad=bc\)
\(\Rightarrow ad:cd=bc:cd\) (hai số bằng nhau cùng chia cho một số thì vẫn bằng nhau)
\(\Leftrightarrow\frac{ad}{cd}=\frac{bc}{cd}\)
Từ đó ta có tỉ lệ thức \(\frac{a}{c}=\frac{b}{d}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
chứng minh rằng từ đẳng thức ad = bc ( c , d khác 0 ) ta suy a được tỉ lệ thức a / c = b / d
Do ad = bc
=> \(\frac{ad}{cd}=\frac{bc}{cd}\)
=> \(\frac{a}{c}=\frac{b}{d}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Do ad = bc
\(\Rightarrow\frac{a}{d}=\frac{b}{c}\)
\(\Rightarrow ac=bd\)
\(\Rightarrow\frac{a}{c}=\frac{b}{d}\left(\text{đ}pcm\right)\)
Đúng 0
Bình luận (0)
Giải:
Ta có: ad = bc
\(\Rightarrow\) ad : cd = bc : cd
\(\Rightarrow\) a : c = d : d
\(\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Vậy \(\frac{a}{c}=\frac{b}{d}\)
Đúng 0
Bình luận (0)
Chứng minh rằng từ đẳng thức ad = bc ( c,d \(\ne\) 0 ), ta có thể suy ra được tỉ lệ thức \(\dfrac{a}{c}=\dfrac{b}{d}\)
Ta có :
\(ad=bc\left(1\right)\)
Chia cả 2 vế của \(\left(1\right)\) cho \(bd\) ta được :
\(VT=\dfrac{ad}{bd}=\dfrac{a}{b}\left(2\right)\)
\(VP=\dfrac{bc}{bd}=\dfrac{c}{d}\left(3\right)\)
Từ \(\left(2\right)+\left(3\right)\Leftrightarrowđpcm\)
Đúng 0
Bình luận (0)
Từ có đẳng thức: \(ad=bc\)
\(\Rightarrow\dfrac{ad}{cd}=\dfrac{bc}{cd}\) \(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\) (đpcm)
Đúng 0
Bình luận (0)
Chứng minh rằng từ đẳng thức ad=bc ( c,d \(\ne\) 0 ) ta có thể suy ra được tỉ lệ thức \(\frac{a}{b}=\frac{c}{d}\)
Ta có: ad=bc (1)
Chia 2 vế của (1) cho bd ta có:
\(VT=\frac{ad}{bd}=\frac{a}{b}\left(2\right)\)
\(VP=\frac{bc}{bd}=\frac{c}{d}\left(2\right)\)
Từ (1) và (2) ta có: \(\frac{a}{b}=\frac{c}{d}\)
Đúng 0
Bình luận (0)


























