cho tam giác ABC. Vẽ ra phía ngoài tam giác các hình vuông BCKL, BAED. Chứng minh :
a) DL = 2BM ( M là trung điểm của AC)
b)Kẻ đường cao AH của tam giác ABC, chứng minh AH đi qua trung điểm của DL
Những câu hỏi liên quan
cho tam giác ABC. Vẽ ra phía ngoài tam giác các hình vuông BCKL, BAED. Chứng minh :
a) DL = 2BM ( M là trung điểm của AC)
b)Kẻ đường cao AH của tam giác ABC, chứng minh AH đi qua trung điểm của DL
Cho tam giác ABC, M là trung điểm của AC. Phía ngoài tam giác ABC dựng hình vuông BCKL, ABDE. Lấy điểm Q trên tia đối của tia MB sao cho MBMQ
Chứng minh:
a)DLBQ
b)DLBM
Đọc tiếp
Cho tam giác ABC, M là trung điểm của AC. Phía ngoài tam giác ABC dựng hình vuông BCKL, ABDE. Lấy điểm Q trên tia đối của tia MB sao cho MB=MQ
Chứng minh:
a)DL=BQ
b)DL=BM
a/
MA=MC (gt); MB=MQ (gt) => ABCQ là hbh (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường)
=> AQ=BC (cạnh đối hbh) (1)
\(\widehat{ABC}=\widehat{AQC}\) (góc đối hbh) (2)
Ta có BL=BC (cạnh hình vuông) (3)
Ta có
\(\widehat{DBL}+\widehat{ABC}=360^o-\widehat{ABD}-\widehat{LBC}=360^o-90^o-90^o=180^o\left(4\right)\)
\(\widehat{BAQ}+\widehat{AQC}=180^o\) (5)
Xét \(\Delta BDL\) và \(\Delta ABQ\) có
BD=AB (cạnh hình vuông)
Từ (1) và (3) => BL=AQ
Từ (2) (4) (5) => \(\widehat{DBL}=\widehat{BAQ}\)
\(\Rightarrow\Delta BDL=\Delta ABQ\) (c.g.c) => DL=BQ
Câu b xem lại đề bài
Đúng 1
Bình luận (0)
cho tam giác abc vẽ phía ngoài tam giác các hình vuông ABDE và BCKL vẽ trng tuyến BM của tam giác ABC.chứng minh DL=2BM
Trên tia đối của tia MB lấy điểm G sao cho BM = MG . Gọi N là trung điểm DL
Dễ dàng chứng minh được BCGA là hình bình hành => AB = CG = BD ;
Ta có : Góc DBL + góc ABC = 360 độ - 90 độ - 90 độ = 180 độ
mà BCGA là hình bình hành => AB // CG => góc ABC + góc GCB = 180 độ
=> góc DBL = góc BCG
Xét tam giác DBL và tam giác BCG có BC = BL (BCKL là hình vuông)
góc DBL = góc BCG (cmt) ; CG = DB
=> tam giác DBL = tam giác BCG (c.g.c)
=> BG = DL => DL = 2BM
Đúng 0
Bình luận (0)
cho tam giác abc. Vẽ về phía ngoài của tam giác các hình vuông abde , acfg.
a) chứng minh đường cao ah của tam giác abc đi qua trung điểm m của đoạn eg
b) cmr nếu góc a<90 độ và n là trung điểm của df thì tam giác nbc vuông cân tại đỉnh n
Cho tam giác ABC. Về phía ngoài tam giác dựng các hình vuông ABDE, ACFG. Chứng minh rằng đường cao AH của tam giác ABC đi qua trung điểm M của đoạn thẳng EG.
Cho tam giác ABC. Vẽ về phía ngoài của tam giác ABC các tam giác vuông tại A là ABD, ACE có AB= AD, AC=AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. CHứng minh rằng :
a) DM= AH
b) DM đi qua trung điểm của DE.
Cho tam giác ABC. Vẽ ở phía ngoài tam giác ABC các tam giác vuông tại A và ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng: MN đi qua trung điểm của DE
Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180o(kề bù)
Mà ∠(CAE) =90o⇒∠(HAC) +∠(EAN) =90o (4)
Trong tam giác vuông AHC, ta có:
∠(AHC) =90o⇒∠(HAC) +∠(HCA) =90o (5)
Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂
Xét hai tam giác vuông AHC và ENA, ta có:
∠(AHC) =∠(ENA) =90o
AC = AE (gt)
∠(HCA) =∠(EAN) ( chứng minh trên)
Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)
Vậy AH = EN (hai cạnh tương ứng)
Từ (3) và (6) suy ra: DM = EN
Vì DM ⊥ AH và EN ⊥ AH (giả thiết) nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
Gọi O là giao điểm của MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
∠(DMO) =∠(ENO) =90o
DM= EN (chứng minh trên)
∠(MDO) =∠(NEO)(so le trong)
Suy ra : ΔDMO= ΔENO(g.c.g)
Do đó: DO = OE ( hai cạnh tương ứng).
Vậy MN đi qua trung điểm của DE
Đúng 0
Bình luận (0)
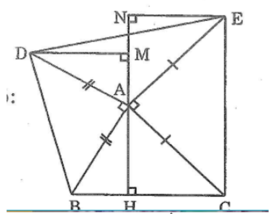
Cho tam giác Abc, vẽ phía ngoài tam giác ABC các tam giác vuông tại A là tam giác ABD;tam giác ACE; có AB =AD; AC=AE. kẻ AH vuông góc BC; DM vuông góc ANH; EN vuông góc AH. chứng minh: a) DM = AH; b) MN đi qua trung điểm DE
Cho tam giác ABC. Vẽ về phía ngoài tam giác ABC các tam giác vuông tại A là ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng :
a) DM = AH
b) MN đi qua trung điểm của DE
a) Ta có ˆBAH+ˆBAD+ˆDAM=180∘BAH^+BAD^+DAM^=180∘ (kề bù)
Mà ˆBAD=90∘⇒ˆBAH+ˆDAM=90∘BAD^=90∘⇒BAH^+DAM^=90∘ (1)
Trong tam giác vuông AMD, ta có:
ˆAMD=90∘⇒ˆDAM+ˆADM=90∘(2)AMD^=90∘⇒DAM^+ADM^=90∘(2)
Từ (1) và (2) suy ra: ˆBAH=ˆADMBAH^=ADM^
Xét hai tam giác vuông AMD và BHA, ta có:
ˆAMD=ˆBAH=90∘AMD^=BAH^=90∘
AB = AD (gt)
ˆBAH=ˆADMBAH^=ADM^ (chứng minh trên)
Suy ra: ∆AMD = ∆BHA (cạnh huyền, góc nhọn)
Vậy: AH = DM (2 cạnh tương ứng) (3)
b) Ta có: ˆHAC+ˆCAE+ˆEAN=180∘HAC^+CAE^+EAN^=180∘ (kề bù)
Mà ˆCAE=90∘(gt)⇒ˆHAC+ˆEAN=90∘CAE^=90∘(gt)⇒HAC^+EAN^=90∘ (4)
Trong tam giác vuông AHC, ta có:
ˆAHC=90∘⇒ˆHAC+ˆHCA=90∘(5)AHC^=90∘⇒HAC^+HCA^=90∘(5)
Từ (4) và (5) suy ra: ˆHCA=ˆEANHCA^=EAN^
Xét hai tam giác vuông AHC và ENA, ta có:
ˆAHC=ˆENA=90∘AHC^=ENA^=90∘
AC = AE (gt)
ˆHCA=ˆEANHCA^=EAN^ (chứng minh trên)
Suy ra: ∆AHC = ∆ENA (cạnh huyền, góc nhọn)
Vậy AH = EN (2 cạnh tương ứng)
Từ (3) và (6) suy ra : DM = EN
Vì DM⊥AHDM⊥AH và EN⊥AHEN⊥AH nên DM // EN (2 đường thẳng cùng vuông góc đường thẳng thứ 3)
Gọi O là giao điểm MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
ˆDMO=ˆENO=90∘DMO^=ENO^=90∘
DM = EN (chứng minh trên)
ˆMDO=ˆNEOMDO^=NEO^ (so le trong)
Suy ra: ∆DMO = ∆ENO (g.c.g) => OD = DE
Vậy MN đi qua trung điểm của DE.
Đúng 0
Bình luận (0)