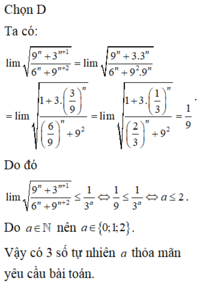a: \(\Leftrightarrow n+2=6\)

hay n=4

a:  hay n = 4

a) \(\left(n+2\right)+6⋮\left(n+2\right)\Rightarrow\left(n+2\right)\inƯ\left(6\right)=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)

Do \(n\in\) N*, n>1  \(\Rightarrow n\in\left\{4\right\}\)

b) Gọi d là \(UCLN\left(9n+11;12n+15\right)\)

\(\Rightarrow\left\{{}\begin{matrix}\left(9n+11\right)⋮d\\\left(12n+15\right)⋮d\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(36n+44\right)⋮d\\\left(36n+45\right)⋮d\end{matrix}\right.\)

\(\Rightarrow\left(36n+45\right)-\left(36n+44\right)⋮d\Rightarrow1⋮d\Rightarrowđpcm\)

Vậy 2 số trên luôn là 2 số nguyên tố cùng nhau

\(9n^2+9n-8=(3n)^2+6n+1+3n-9 = (3n+1)^2+(3n-9) để là số chính phương thì 3n-9=0=> n=3 \)

Ta đặt :

\(\hept{\begin{cases}4n+5=a^2\\9n+7=b^2\end{cases}}\)( a,b là các số tự nhiên )

\(\Rightarrow\hept{\begin{cases}36n+45=9a^2\\36n+28=4b^2\end{cases}}\)

\(\Rightarrow\left(36n+45\right)-\left(36n+28\right)=9a^2-4b^2\)

\(\Rightarrow17=\left(3a-2b\right)\left(3a+2b\right)\)

Vì a, b là các số tự nhiên nên 3a-2b , 3a+3b là cá số nguyên và 3a-2b <= 3a+2b nên ta có 

\(\left(3a-2b;3a+2b\right)\in\left\{\left(1;17\right);\left(-17;-1\right)\right\}\)

\(\Rightarrow6a\in\left\{18;-18\right\}\)

\(\Rightarrow a\in\left\{3;-3\right\}\)

Mà a là số tự nhiên nên a=3

\(\Rightarrow4n+5=a^2=3^2=9\)

\(\Rightarrow4n=4\)

\(\Rightarrow n=1\)

        Vậy n=1