tham khảo

Trên tia đối tia CD lấy điểm M sao cho CM = AK

Ta có: AK + CE = CM + CE = EM (*)

Xét ∆ ABK và ∆ CBM:

AB = CB (gt)

ˆA=ˆC=900

AK = CM (theo cách vẽ)

Do đó: ∆ ABK = ∆ CBM (c.g.c)

⇒ˆB1=ˆB4

(1)

ˆKBC=900–ˆB1

(2)

Trong tam giác CBM vuông tại C.

ˆM=900–ˆB4

(3)

Từ (1), (2) và (3) suy ra: ˆKBC=ˆM

(4)

ˆKBC=ˆB2+ˆB3

 mà  ˆB1=ˆB2

(gt)

ˆB1=ˆB4

(chứng minh trên)

Suy ra: ˆB2=ˆB4⇒ˆB2+ˆB3=ˆB3+ˆB4

hay ˆKBC=ˆEBM

(5)

Từ (4) và (5) suy ra: ˆEBM=ˆM

⇒ ∆ EBM cân tại E ⇒ EM = BE (**)

Từ (*) và (**) suy ra: AK + CE = BE

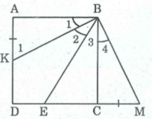
Trên tia đối của tia CD lấy điểm M sao cho CM = AK

Ta có: AK + CE = CM + CE = EM (1)

Xét ∆ ABK và  ∆ CBM, ta có:

AB = CB (gt)

∠ A = ∠ C = 90 0

AK = CM (theo cách vẽ)

Suy ra:  ∆ ABK = ∆ CBM (c.g.c)

⇒  ∠ B 1  =  ∠ B 4  (2)

Lại có:  ∠ B 1 = ∠ B 2  ( do BK là tia phân giác của ABE)

Suy ra:  ∠ B 1  =  ∠ B 2  =  ∠ B 4

Mà  ∠ (KBC) =  90 0  -  ∠ B 1  (3)

Tam giác CBM vuông tại C nên:  ∠ M =  90 0  -  ∠ B 4  (4)

Từ (2), (3) và (4) suy ra:  ∠ (KBC) =  ∠ M (5)

Hay  ∠ B 2 +  ∠ B 3  =  ∠ M

⇒  ∠ B 4  +  ∠ B 3  =  ∠ M( vì  ∠ B 2  =  ∠ B 4  )

Hay:  ∠ (EBM) =  ∠ M

⇒  ∆ EBM cân tại E ⇒ EM = BE. (6)

Từ (1) và (6) suy ra: AK + CE = BE.

trên tia đối của AD lấy N sao cho AN = CE 
ta có: 
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau) 
=> CBE^ = ABN^ (1) 
BK là phân giác của ABE^ nên: 
KBE^ = KBA^ (2) 
(1) + (2) được: 
CBE^ + KBE^ = ABN^ + KBA^ 
=> CBK^ = KBN^ (*) 
mà: CBK^ = BKN^ (**) ( so le trong) 
(*) và (**) => BKN^ = KBN^ => BNK là tam giác cân tại N 
=> NB = NK 
=> NB = AN + AK = CE + AK (3) 
do: Δ BCE = Δ BAN => BE = NB (4) 
(3) và (4) => CE + AK = BE

ta có: 
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau) 
=> CBE^ = ABN^ (1) 
BK là phân giác của ABE^ nên: 
KBE^ = KBA^ (2) 
(1) + (2) được: 
CBE^ + KBE^ = ABN^ + KBA^ 
=> CBK^ = KBN^ (*) 
mà: CBK^ = BKN^ (**) ( so le trong) 
(*) và (**) => BKN^ = KBN^ => BNK là tam giác cân tại N 
=> NB = NK 
=> NB = AN + AK = CE + AK (3) 
do: Δ BCE = Δ BAN => BE = NB (4) 
(3) và (4) => CE + AK = BE
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
li-ke cho minhf nhes bn Nguyễn Thị Thùy Trang

Bài 3: 

Xét ΔCBD có CD=CB

nên ΔCBD cân tại C

Suy ra: \(\widehat{CDB}=\widehat{CBD}\)

mà \(\widehat{CDB}=\widehat{ADB}\)

nên \(\widehat{ADB}=\widehat{DBC}\)

mà hai góc này ở vị trí so le trong

nên AD//BC

hay ADCB là hình thang