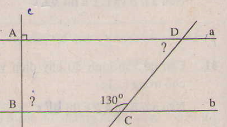
Xem hình 31 :
a) Vì sao a // b ?
b) Tính số đo góc C.
m.n giúp mình nha ![]()
Xem hình 31
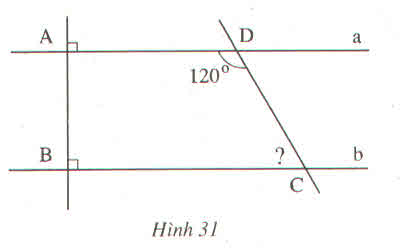
a) Vì sao a // b ?
b) Tính số đo góc C ?
a, Ta có:
AB \(\perp\) a
AB \(\perp\) b
\(\Rightarrow\)a // b
b, Ta có: a // b( câu a)
hai góc ADC và DCB là hai góc trong cùng phía
\(\Rightarrow\)DCB = 180\(^0\) - ADC(tính chất hai đường thẳng song song)
\(\Rightarrow\) DCB = 180\(^0\)-120\(^0\) = 60\(^0\)
a, Ta có:
+ góc DAB = 90o
+ góc CBA = 90o
=> a//b ( 2 đoạn thẳng cx vuông góc vs 1 đoạn thẳng)
b, Vì a//b ( theo a) nên
=> góc C = 180o - 120o = 60o.
Vậy góc C = 60o
A) tam giác ABC cân tại A, có góc B = 75 . tính số góc của góc A
b) tam giác MNP cân tại P. Biết góc P có số đo góc = 100. Tính số đo góc của N
c) tam giác MNP có MN = 5cm, MP =12 cm , NP = 13 cm . Hỏi tam giác MNP có phải là tam giác vuông ko vì sao
MÌNH YẾU MÔN TOÁN LẮM MÀ TUẦN NÀY PHẢI NỘP CHO CÔ RỒI
MÌNH MONG MỌI NG GIÚP MÌNH VỚI NHA
a) Từ \(\Delta ABC\)cân tại A, \(\Rightarrow\widehat{B}=\widehat{C}=75^o\)
\(\Rightarrow\widehat{A}=180^o-\left(\widehat{B}+\widehat{C}\right)\)
\(\Rightarrow\widehat{A}=180^o-\left(75^o+75^o\right)\)
\(\Rightarrow\widehat{A}=30^o\)
b) Từ \(\Delta MNP\)cân tại P, \(\Rightarrow\widehat{M}=\widehat{N}=\frac{180^o-\widehat{P}}{2}=\frac{80^o}{2}=40^o\)
c) Ta có: \(NP^2=13^2=169\)(1)
\(MN^2+MP^2=5^2+12^2=25+144=169\)(2)
Từ (1) và (2) suy ra: \(NP^2=MN^2+MP^2\)
\(\Rightarrow\Delta MNP\)vuông (theo định lí Pytago)
Happy new year!!!
Xem hình 60 :
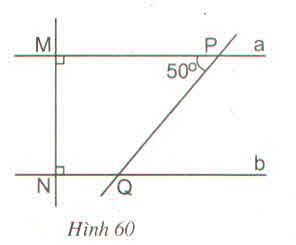
a) Giải thích vì sao a // b
b) Tính số đo góc NQP
a) Hai đường thẳng a và b cùng vuông góc với đường thẳng MN nên a // b.
b) Ta có góc MPQ = góc Q1 = 50o (so le trong vì a // b)
mà góc Q1 + Q2 = 180o (kề bù)
=> Q2 = 180o - 50o = 130o
Vậy góc NQP = 130o.
Kí hiệu như hình vẽ.
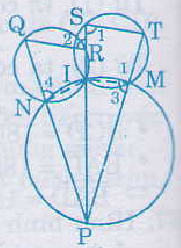
Ta có tứ giác ISTM nội tiếp đường tròn nên:
+ = 180o
Mà + = 180o (kề bù)
nên suy ra = (1)
Tương tự từ các tứ giác nội tiếp IMPN và INQS ta được
= (2)
= (3)
Từ (1), (2), (3) suy ra
Do đó QR // ST
vẽ xoy và yoz kế bù ,sao cho xoy = 130* ...
a) tính số đo của góc yoz?
b) vẽ tia ot nằm trong xoz ,sao cho xot = 80* . tính số đo của góc yot ?
c) tia oy có phải là tia phân giác của yoz không ? vì sao?
( mình đang cần gấp , giúp mình nha)
a) Vì xOy kề bù với yOz:
nên: xOy+yOz=xOz
hay:130*+yOz=180*
=> yOz=180*-130*
Vậy yOz=50*
b) Vì xOt kề bù với yOt:
nên: xOt+yOt=xOy
hay:80*+yOt=130*
=> yOt=130*-80*
Vậy yOt=50*
c) Oy là tia phân giác cảu góc tOz vì:
\(tOy=yOz=\frac{1}{2}tOz\)
Vậy Oy là tia phân giác của góc tOz.
(Bài làm ko hiểu cứ hỏi mk nhé ![]() ^...^
^...^ ![]() ^_^)
^_^)
a) Ta có:
\(\widehat{xOy} + \widehat{yOz} = 180^O\) (kề bù)
\(130^O + \widehat{yOz} = 180^O (\widehat{xOy} = 130^O(gt))\)
\(\widehat{yOz} = 180^O - 130^O\)
\(\widehat{yOz} = 50^O\)
Vậy \(\widehat{yOz} = 50^O\)
b) Ta có:
\(\widehat{xOt} + \widehat{tOy} = \widehat{xOy}\) (Ot nằm giữa Ox và Oy)
\(80^O + \widehat{tOy} = 130^O (\widehat{xOt} = 80^O (gt); \widehat{xOy} = 130^O(gt))\)
\(\Rightarrow\)\(\widehat{tOy} = 130^O - 80^O\)
\(\widehat{tOy} = 50^O\)
Vậy \(\widehat{tOy} = 50^O\)
c) Ta có:
Oy nằm giữa hai tia Ot và Oz
mà \(\widehat{tOy} = \widehat{yOz} (=50^O)\)
\(\Rightarrow\) Oy là tia phân giác của \(\widehat{tOz}\)
ta có xoy+yoz=1800(kề bù)
1300+yoz=1800
yoz=50o
b) ta có yot+xot=yox
yot+80=130o
yot=50o
c) viết sai đề bài rồi tia oy phải là phân giác của zot chứ
B1 : My // Ax , yMC =30 độ , MCA = 48 độ , Az là tia p/g CAt . Tính số đo góc tAz ( vẽ hình giúp em ạ )
B2 : a // b , A = 30 độ , B = 40 độ . Tính số đo góc AOB . Nói rõ vì sao tính đc như thế ? ( vẽ hình cho em với ạ )
Cho 2 góc kề bù AOB và BOC, trong đó BOC=50°. Trên nửa mặt phẳng BAC có chứa toa OB ta vẽ tia OD. Sao cho góc AOD=80°
a) Tính số đo góc COD
b) Tia OB có nằm giữa 2 tia OC và OD không? Vì sao?
c) Tia OB có phải là tia phân giác của gócCOD không? Vì sao?
Giúp mình nha! Trình bày câu a), b), c) ko thôi khỏi vẽ hình cũng được. Cảm ơn trước nhé!
Cho hình vẽ:
a) Vì sao a // b?
b) Tính số đo góc D ^ ?
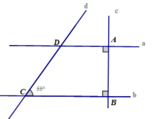
Cho hình vẽ:
a) Ta có a ⊥ c và b ⊥ c => a // b
b) Ta có: C ^ + D ^ = 180 0 (cặp góc kề bù)
D ^ = 180 0 − 55 0 = 125 0
cho góc bẹt xOy. Vẽ tia Ot sao cho góc yOt=40độ
a)tính số đo góc xOt
b) trên nửa mặt phẳng bờ xy chứa tia Ot vẽ tia Om sao cho góc xOm=100 độ.tia ot có phải là tia phân giác của góc yOm không ? Vì sao?
giúp mình nha mình cần gấp tối nay thank
1234567890-0987654321
0987654321-11223344555566778990
122346677990+1223445556778890
11223456678899009-1222334445677890098
113445678+12344556677899999
Cho tam giác ABC vuông cân tại A . Trên tia đối của tia BA lấy điểm E sao cho BE=BC.
a) Tính số đo các góc của AEC
b) Trên tia đối của tia BC lấy điểm F sao cho BF=BC . Tính số đo các tam giác CEF
giúp mình đi !!! Nhanh lên giúp mình Vẽ hình luôn nha
b: \(\widehat{CBE}=180^0-45^0=135^0\)
\(\Leftrightarrow\widehat{BCE}=\dfrac{180^0-135^0}{2}=22.5^0\)
hay \(\widehat{CFE}=67.5^0\)
a: \(\widehat{AEC}=\dfrac{180^0-135^0}{2}=22.5^0\)