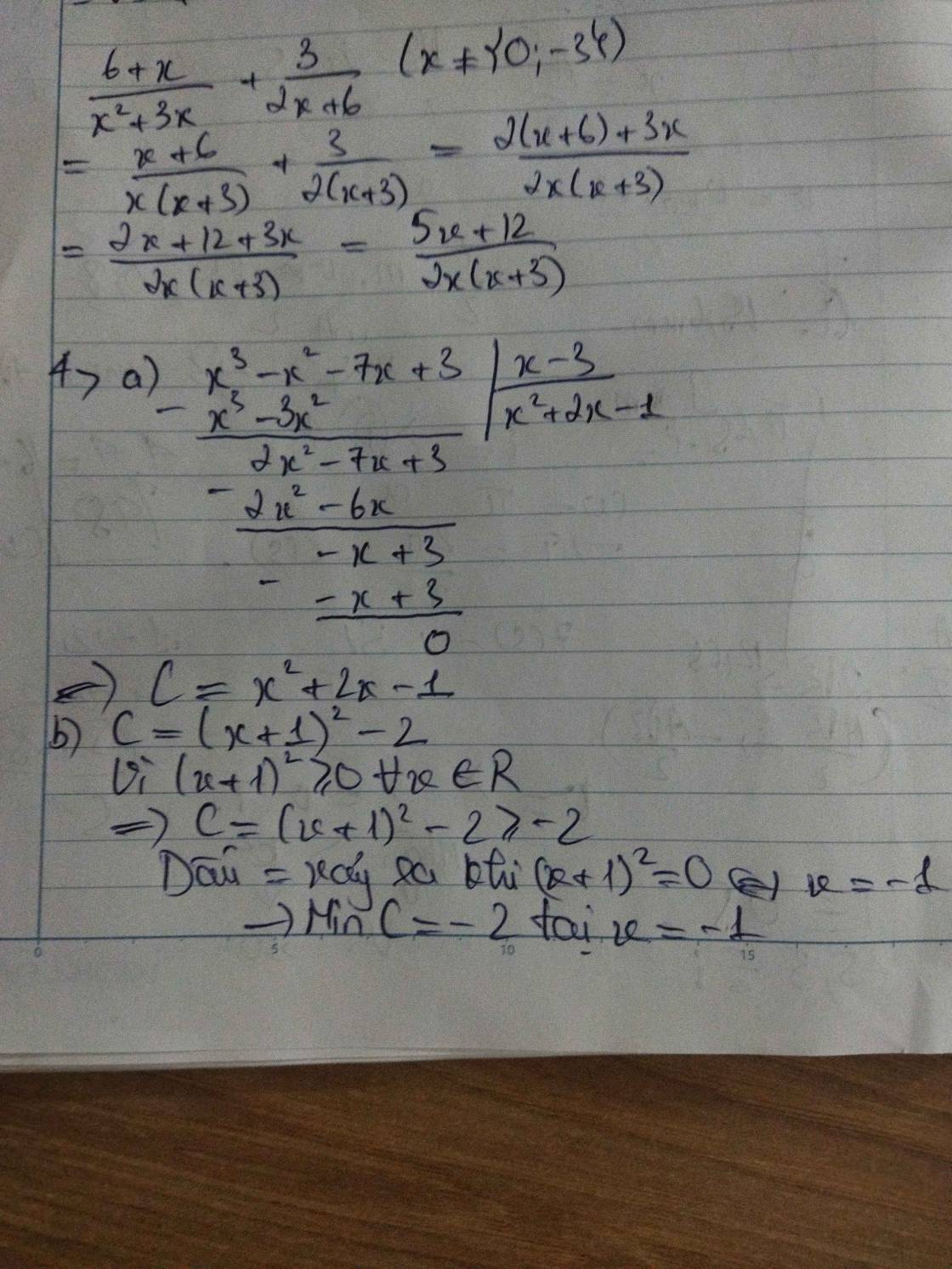tìm giá trị nhỏ nhất của đa thức : -3x (x+3)-7

Những câu hỏi liên quan
Tìm giá trị lớn nhất của đa thức: D = -3X (X+3) -7
Tìm giá trị nhỏ nhất của đa thức: A= X^2 + 5X +8
B= x (x trừ 6)
tìm giá trị nhỏ nhất của đa thức : -3x (x+3)-7
\(-3x\left(x+3\right)-7\)
\(=-3x^2-9x-7\)
\(=-\left(\sqrt{3}x\right)^2-2\sqrt{3}x.\frac{9}{2\sqrt{3}}-\frac{81}{12}+\frac{81}{12}-7\)
\(=-\left(\sqrt{3}x+\frac{9}{2\sqrt{3}}\right)^2-\frac{1}{4}\)
vì \(-\left(3x+\frac{9}{2\sqrt{3}}\right)^2\le0\)
Nên\(-\left(3x+\frac{9}{2\sqrt{3}}\right)-\frac{1}{4}\le-\frac{1}{4}\)
Vậy GTNN của đa thức trên là: \(-\frac{1}{4}\)
Đúng 0
Bình luận (1)
Tìm giá trị nhỏ nhất của đa thức x^2-3x
Tìm giá trị lớn nhất của đa thức -x^2-2x
Đặt \(A=x^2-3x\)
\(A=\left(x^2-3x+\frac{9}{4}\right)-\frac{9}{4}\)
\(A=\left(x-\frac{3}{2}\right)^2-\frac{9}{4}\)
Mà \(\left(x-\frac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A\ge-\frac{9}{4}\)
Dấu "=" xảy ra khi : \(x-\frac{3}{2}=0\Leftrightarrow x=\frac{3}{2}\)
Vậy \(A_{Min}=-\frac{9}{4}\Leftrightarrow x=\frac{3}{2}\)
Đặt \(B=-x^2-2x\)
\(-B=x^2+2x\)
\(-B=\left(x^2+2x+1\right)-1\)
\(-B=\left(x+1\right)^2-1\)
Mà \(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow-B\ge-1\Leftrightarrow B\le1\)
Dấu "=" xảy ra khi : \(x+1=0\Leftrightarrow x=-1\)
Vậy \(B_{Max}=1\Leftrightarrow x=-1\)
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của đa thức 3x^2+6x+15/x^2+2x+3
\(\dfrac{3x^2+6x+15}{x^2+2x+3}=\dfrac{3\left(x^2+2x+3\right)+6}{x^2+2x+3}\\ =3+\dfrac{6}{x ^2+2x+3}\)
Nhận thấy : \(x^2+2x+3=\left(x+1\right)^2+2\ge2\forall x\)
\(=>\dfrac{6}{x^2+2x+3}\le\dfrac{6}{2}=3\)
\(=>3+\dfrac{6}{x^2+2x+3}\le3+3=6\\ =>\dfrac{3x^2+6x+15}{x^2+2x+3}\le6\)
Dấu = xảy ra khi : x+1=0 hay x=-1
Vậy GTLN của đa thức là : 6 tại x = -1
Đúng 1
Bình luận (0)
tìm giá trị lớn nhất của đa thức D=-3x(x+3)-7
\(\dfrac{6+x}{x^2+3x}+\dfrac{3}{2x+6}\)
\(4\)).Cho đa thức A= \(x^3-x^2-7x+3\) và đa thức B= \(x-3\)
a. Tìm C= A:B
b.Tìm giá trị nhỏ nhất của C
1. Giá trị lớn nhất của -17- (x-3)^22.Giá trị nhỏ nhất của biểu thức A x(x+1) +3/23.Giá trị lớn nhất của biểu thức A -2x^2 +5 -54.Giá trị nhỏ nhất của 3x^2 +2x +28/35.Giá trị của x để x^2 -48x +65 đạt giá trị nhỏ nhất6.GIá trị của x để biểu thức B3 - x^2 +2x7.Giá trị của x để 3(2x +9)^2 -1 đạt giá trị nhỏ nhất8.Hệ số của x trong khai triển của đa thức (1/2x +2 )^2Ai giúp mình với !
Đọc tiếp
1. Giá trị lớn nhất của -17- (x-3)^2
2.Giá trị nhỏ nhất của biểu thức A= x(x+1) +3/2
3.Giá trị lớn nhất của biểu thức A = -2x^2 +5 -5
4.Giá trị nhỏ nhất của 3x^2 +2x +28/3
5.Giá trị của x để x^2 -48x +65 đạt giá trị nhỏ nhất
6.GIá trị của x để biểu thức B=3 - x^2 +2x
7.Giá trị của x để 3(2x +9)^2 -1 đạt giá trị nhỏ nhất
8.Hệ số của x trong khai triển của đa thức (1/2x +2 )^2
Ai giúp mình với !
\(1.\)
\(-17-\left(x-3\right)^2\)
Ta có: \(\left(x-3\right)^2\ge0\)với \(\forall x\)
\(\Leftrightarrow-\left(x-3\right)^2\le0\)với \(\forall x\)
\(\Leftrightarrow17-\left(x-3\right)^2\le17\)với \(\forall x\)
Dấu '' = '' xảy ra khi:
\(\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Vậy \(Max=-17\)khi \(x=3\)
\(2.\)
\(A=x\left(x+1\right)+\frac{3}{2}\)
\(A=x^2+x+\frac{3}{2}\)
\(A=\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
\(\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
\(\Leftrightarrow\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
Vậy \(Max=\frac{5}{4}\)khi \(x=\frac{-1}{2}\)
\(5.\)
\(x^2-48x+65\)
\(=\left(x-24\right)^2\ge0\)với \(\forall x\)
\(\left(x-24\right)^2\ge0\)với \(\forall x\)
\(\Leftrightarrow\left(x-24\right)^2-511\ge-511\)với \(\forall x\)
Vậy \(Max=-511\)khi \(x=24\)
Xem thêm câu trả lời
Tìm giá trị lớn nhất hoặc nhỏ nhất của đa thức sau:
\(\dfrac{31}{x^2-3x+11}+15\)
Lời giải:
Ta có:
$x^2-3x+11=(x-\frac{3}{2})^2+\frac{35}{4}\geq \frac{35]{4}$
$\Rightarrow \frac{31}{x^2-3x+11}\leq 31:\frac{35}{4}=\frac{124}{35}$
$\Rightarrow \frac{31}{x^2-3x+11}+15\leq \frac{649}{35}$
Vậy gtln của biểu thức là $\frac{649}{35}$ khi $x=\frac{3}{2}$
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất của đa thức :
D = -3x ( x + 3 ) - 7
D=-3x(x+3)-7
D=-3x² - 9x - 7
D=3x² - 3.2.x.3/2-27/4-1/4
D=3.(x²-2x.3/2-9/4)-1/4
D=3.(x-3/2)²-1/4 < hoặc = - 1/4 vì -3.(x-3/2)²< hoặc = 0
Dấu = xảy ra khi:
X-3/2=0
X=3/2
Vậy GTLN của D là-1/4 tại x=3/2
Tích nha
Đúng 0
Bình luận (0)
Giá trị lớn nhất của D = -3x ( x + 3 ) - 7 là -1/2
Đúng 0
Bình luận (0)
3x+7=28
3x =28-7
3x =21
x =21:3
x =7
Đúng 0
Bình luận (0)