biểu diễn số hữu tỉ \(\frac{3}{-4}\) trên trục số

Những câu hỏi liên quan
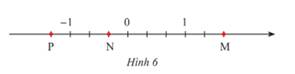
a) Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?
b) Biểu diễn các số hữu tỉ sau trên trục số: \( - 0,75;\,\frac{1}{{ - 4}};\,1\frac{1}{4}.\)
a) Các điểm M, N, Q biểu diễn lần lượt các số hữu tỉ:\(\frac{5}{3};\,\frac{{ - 1}}{3};\,\frac{{ - 4}}{3}\).
b)

Đúng 0
Bình luận (0)
Điểm P biểu diễn: \(-\dfrac{4}{3}\)
Điểm N biểu diễn: \(-\dfrac{1}{3}\)
Điểm M biểu diễn: \(\dfrac{5}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Biểu diễn các số hữu tỉ:\(\frac{3}{-4},\frac{5}{3}\)trên trục số
biểu diễn số hữu tỉ \(\frac{3}{-4}\)trên trục số
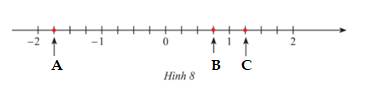
a) Các điểm A,B,C trong Hình 8 biểu diễn số hữu tỉ nào?
b) Biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số.
a) Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)
b) Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)
Vậy ta biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số như sau:

Đúng 0
Bình luận (0)
Biểu diễn các số hữu tỉ sau trên trục số: \( - \frac{1}{2};1;1,25;\frac{7}{4}\)
Nêu 3 cách của số hữu tỉ \(\frac{-3}{5}\)và biểu diễn số hữu tỉ đó trên trục số
cách 1: \(\frac{-3}{5}\)(cách viết dạng phân số)
cách 2: (-3) : 5 ( cách viết dạng phép chia)
cách 3: -0,6 ( cách viết dạng số thập phân)
Đúng 0
Bình luận (0)
nêu 3 cách viết của số hữu tỉ \(\frac{-3}{5}\) và biểu diễn số hữu tỉ đó trên trục số
-0,6; \(\frac{-6}{10}\); \(\frac{-9}{15}\)
Đúng 0
Bình luận (0)
Biểu diễn số hữu tỉ 3 - 4 trên trục số.
Biểu diễn trên trục số:
Ta viết: 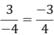
Chia đoạn thẳng đơn vị thành 4 phần bằng nhau , ta được đơn vị mới bằng 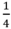 đơn vị cũ.
đơn vị cũ.
Số hữu tỉ 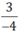 được biểu diễn bởi điểm A nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới
được biểu diễn bởi điểm A nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới

Đúng 0
Bình luận (0)
Biểu diễn số hữu tỉ \(\frac{7}{{10}}\) trên trục số.



















