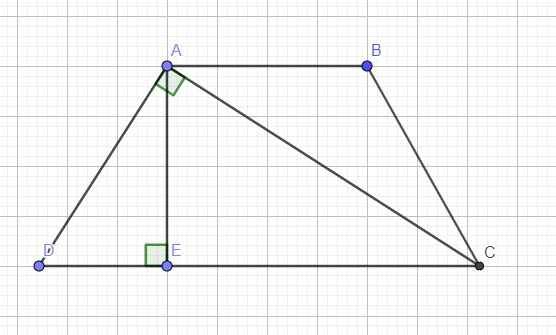
Cho một hình thang cân có đường chéo vuông góc với cạnh bên. Biết đáy nhỏ dài 14cm; đáy lớn dài 50cm. Diện tích của hình thang đó bằng ... .

Những câu hỏi liên quan
Cho hình thang cân có đường chéo vuông góc với cạnh bên. Tính chu vi và diện tích hình thang , biết rằng đáy nhỏ dài 14cm , đáy lớn dài 50cm.
-Gọi hình thang là ABCD, đáy nhỏ AB, đáy lớn CD, có AC⊥AD.
-Từ đỉnh A kẻ đường cao AH của hình thang. Khi đó, DH = \(\frac{50-14}{2}=18\) (cm) và CH = 50 - 18 = 32 (cm)
-Xét tam giác ACD vuông tại A, đường cao AH có:
\(AH^2=HD.HC=18.32=576\Rightarrow AH=24\)(cm)
-Xét tam giác AHD vuông tại H: \(AD=\sqrt{AH^2+DH^2}=\sqrt{24^2+18^2}=30\) (cm)
-Đã có hết các cạnh và đường cao của hình thang, áp dụng công thức tính ra chu vi và diện tích.
Đúng 0
Bình luận (0)
Câu 1: Cho hình thang cân ABCD (AB//CD), AB=26cm , CD=10cm . AC vuông góc với BC. Tính diện tích hình thang đó.
Câu 2: Một hình thang cân có đường chéo vuông góc với cạnh bên. Tính chu vi và diện tích hình thang đó, biết rằng đáy nhỏ dài 14cm , đáy lớn dài 50cm
Một hình thang cân có đường chéo vuông góc với cạnh bên, cạnh bên và đáy nhỏ cùng bằng 1cm. Tính độ dài đáy lớn và đường chéo của hình thang đó
Một hình thang cân có đường chéo vuông góc với cạnh bên, cạnh bên và đáy nhỏ cùng bằng 1cm. Tính độ dài đáy lớn và đường chéo của hình thang đó
ertgrrrr545454545454545454lo;ơ'n0u
Một hình thang cân có đường chéo vuông góc với cạnh bên, cạnh bên và đáy nhỏ cùng bằng 1cm. Tính độ dài đáy lớn và đường chéo của hình thang đó?
Một hình thang cân có đường chéo vuông góc với cạnh bên,cạnh bên và đáy nhỏ cùng bằng 1 cm.Tính đáy lớn và đường chéo của hình thang.
Một hình thang cân có đường chéo vuông góc với cạnh bên,cạnh bên và đáy nhỏ cùng bằng 1 cm.Tính đáy lớn và đường chéo của hình thang.
Mong mọi người trl ạ!
Cho hình thang cân ABCD đáy lớn CD = 10 cm đáy nhỏ bằng đường cao đường chéo vuông góc với cạnh bên Tính độ dài đường cao của hình thang đó
Sửa đề: Đáy nhỏ bằng nửa đáy lớn và bằng độ dài hai cạnh bên
AB=CD/2=5cm
BD vuông góc BC
=>góc BDC+góc BCD=90 độ
AD=BC=AB=5cm
AB=AD
=>góc ABD=góc ADB
=>góc ADB=góc BDC
=>DB là phân giác của góc ADC
góc BDC+góc BCD=90 độ
=>1/2*góc BCD+góc BCD=90 độ
=>góc BCD=60 độ
=>góc BDC=30 độ
Xét ΔBDC vuông tại B có BD^2+BC^2=CD^2
=>BD=5*căn 3(cm)
Kẻ BH vuông góc CD
=>BH=BD*BC/CD=5/2*căn 3(cm)
Đúng 1
Bình luận (0)
Cho hình thang cân ABCD có đáy lớn 𝐶𝐷 = 10𝑐𝑚, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính diện tích hình thang cân đó.
Kẻ đường cao góc AE \(\Rightarrow AE=AB\)
Lại có ABCD là hình thang cân \(\Rightarrow CD=AB+2DE=AE+2DE\Rightarrow DE=\dfrac{CD-AE}{2}=\dfrac{10-AE}{2}\)
\(EC=AB+DE=AE+DE=AE+\dfrac{10-AE}{2}=\dfrac{AE+10}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACD có:
\(AE^2=DE.EC\Leftrightarrow AE^2=\left(\dfrac{10-AE}{2}\right)\left(\dfrac{10+AE}{2}\right)\)
\(\Leftrightarrow4AE^2=100-AE^2\Rightarrow AE=2\sqrt{5}\) \(\Rightarrow AB=2\sqrt{5}\)
\(S_{ABCD}=\dfrac{1}{2}AE.\left(AB+CD\right)=\dfrac{1}{2}.2\sqrt{5}.\left(2\sqrt{5}+10\right)=...\)
Đúng 0
Bình luận (0)