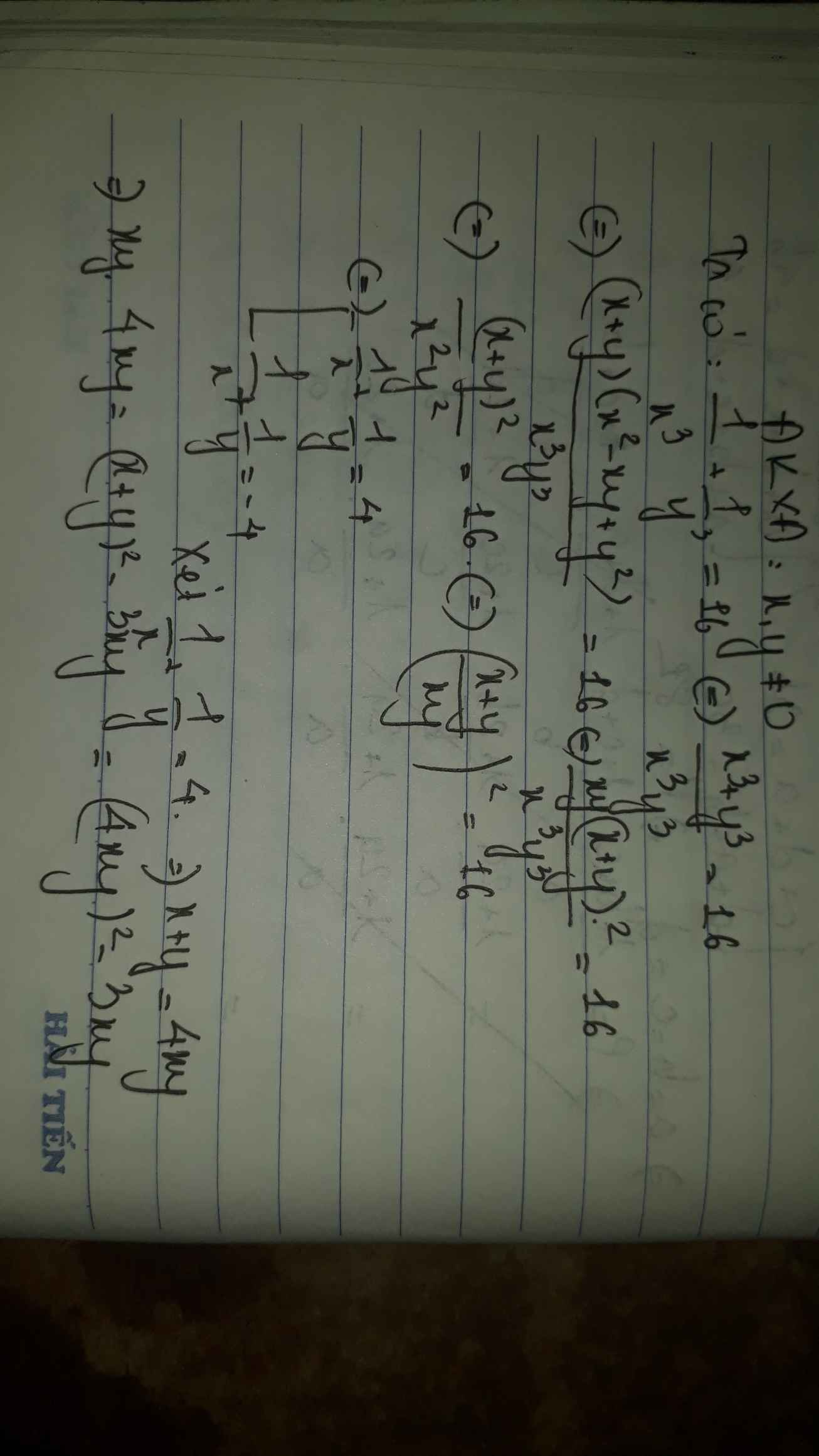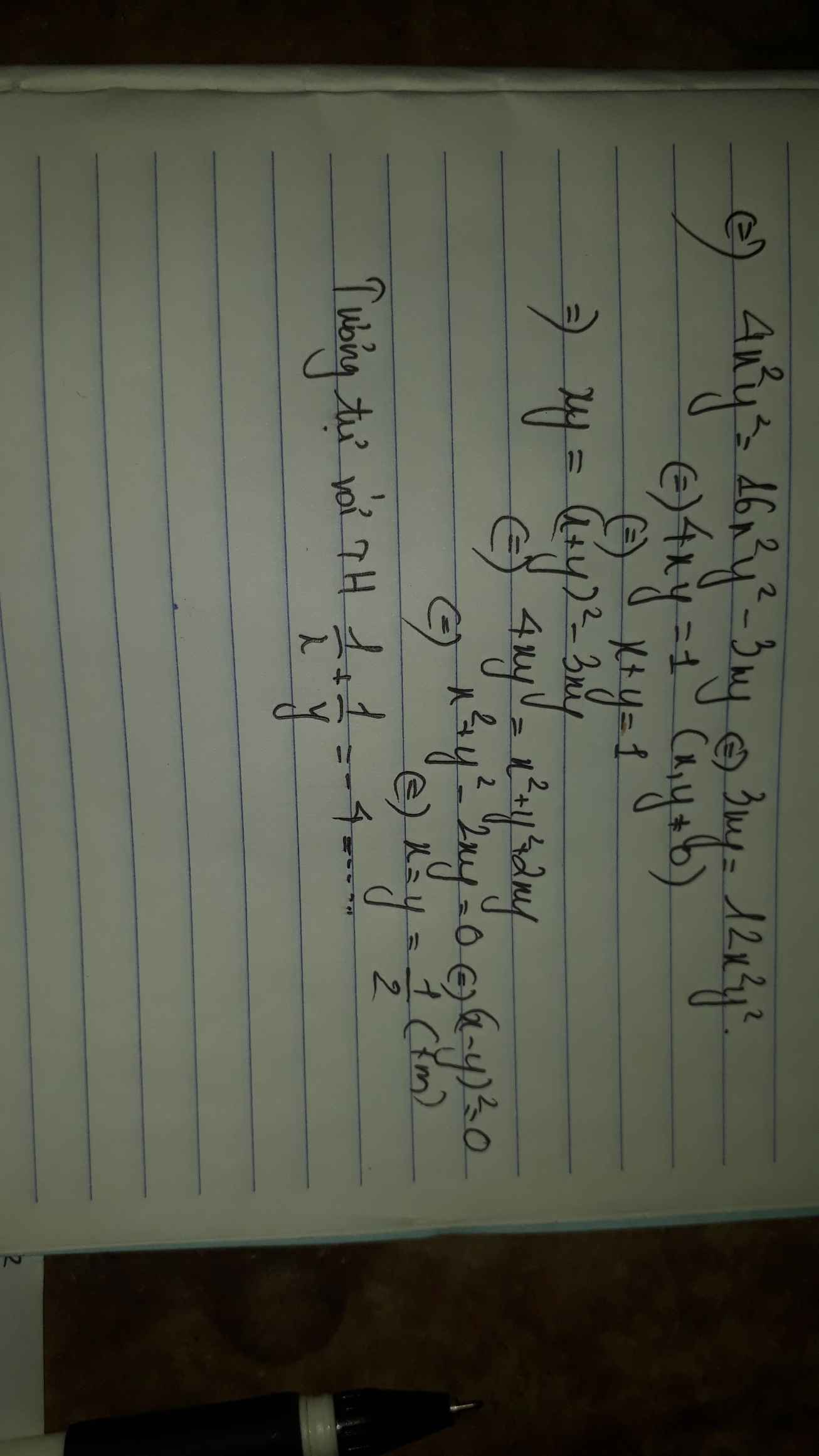a) Ta thấy \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\) và \(x^2+y^2=\left(x+y\right)^2-2xy\) nên nếu đặt \(x+y=S,xy=P\) thì ta có hệ: \(\left\{{}\begin{matrix}S^3-3SP=2\\S^2-2P=2\end{matrix}\right.\) . Từ pt (2) suy ra \(P=\dfrac{S^2-2}{2}\). Thay vào (1), ta có \(S^3-3S.\dfrac{S^2-2}{2}=2\) \(\Leftrightarrow-S^3+6S-4=0\) hay \(S^3-6S+4=0\)

 Đến đây ta dễ dàng nhẩm ra được \(S=2\). Do đó ta lập sơ đồ Horner:

Nghĩa là từ \(S^3-6S+4=0\) ta sẽ có \(\left(S-2\right)\left(S^2+2S-2\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}S=2\\S=-1\pm\sqrt{3}\end{matrix}\right.\).

 Nếu \(S=2\) thì \(P=\dfrac{S^2-2}{2}=1\). Ta thấy \(S^2-4P=0\) nên x, y sẽ là nghiệm của pt \(X^2-2X+1=0\Leftrightarrow\left(X-1\right)^2=0\Leftrightarrow X=1\) hay \(\left(x;y\right)=\left(1;1\right)\).

 Nếu \(S=-1+\sqrt{3}\) thì \(P=\dfrac{S^2-2}{2}=1-\sqrt{3}\). Ta thấy \(S^2-4P>0\) nên x, y là nghiệm của pt \(X^2-\left(\sqrt{3}-1\right)X+1-\sqrt{3}=0\). \(\Delta=2\sqrt{3}\) nên \(X=\dfrac{\sqrt{3}-1\pm\sqrt{2\sqrt{3}}}{2}\) hay \(\left(x;y\right)=\left(\dfrac{\sqrt{3}-1+\sqrt{2\sqrt{3}}}{2};\dfrac{\sqrt{3}-1-2\sqrt{3}}{2}\right)\) và hoán vị của nó. 

 Nếu \(S=-1-\sqrt{3}\) thì \(P=\dfrac{S^2-2}{2}=1+\sqrt{3}\). Mà \(S^2-4P=-2\sqrt{3}< 0\) nên không tìm được nghiệm (x; y)

 Như vậy hệ phương trình đã cho có các cặp nghiệm \(\left(1;1\right);\left(\dfrac{\sqrt{3}-1+\sqrt{2\sqrt{3}}}{2};\dfrac{\sqrt{3}-1-\sqrt{2\sqrt{3}}}{2}\right)\)\(\left(\dfrac{\sqrt{3}-1-\sqrt{2\sqrt{3}}}{2};\dfrac{\sqrt{3}-1+2\sqrt{3}}{2}\right)\)

b) Ta thấy \(x^3+y^3+xy=\left(x+y\right)^3-3xy\left(x+y\right)+xy\)  nên nếu đặt \(S=x+y,P=xy\) thì ta có hệ \(\left\{{}\begin{matrix}S^3-3SP+P=3\\S+P=3\end{matrix}\right.\), suy ra \(P=3-S\) 

\(\Rightarrow S^3-3S\left(3-S\right)+3-S=3\)

\(\Leftrightarrow S^3-10S+3S^2=0\)

\(\Leftrightarrow S\left(S^2+3S-10\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}S=0\\S=2\\S=-5\end{matrix}\right.\)

 Nếu \(S=0\) thì \(P=3\). Khi đó vì \(S^2-4P< 0\) nên không tìm được nghiệm (x; y)

 Nếu \(S=2\) thì suy ra \(P=1\). Ta có \(S^2-4P=0\) nên x, y là nghiệm của pt \(X^2-2X+1=0\Leftrightarrow X=1\) hay \(\left(x;y\right)=\left(1;1\right)\)

 Nếu \(S=-5\) thì suy ra \(P=8\). Ta có \(S^2-4P< 0\) nên không thể tìm được nghiệm (x; y).

 Như vậy hpt đã cho có nghiệm duy nhất \(\left(1;1\right)\)

\(x^3+y^3=5+x^2y+xy^2\Rightarrow x^3+y^3-\left(x^2y+xy^2\right)=5\)

\(\Rightarrow\left(x+y\right)\left(x^2-xy+y^2\right)-xy\left(x+y\right)=5\)

\(\Rightarrow\left(x+y\right)\left(x-y\right)^2=5\)

Vì \(\left\{{}\begin{matrix}\left(x-y\right)^2\ge0\\5>0\end{matrix}\right.\Rightarrow x+y>0\)

Lại có \(\left\{{}\begin{matrix}\left(x-y\right)^2\in N\\\left(x-y\right)^2< 5\end{matrix}\right.\) và \(\left(x-y\right)^2\) là số chính phương

\(\Rightarrow\left(x-y\right)^2=1\Rightarrow\left\{{}\begin{matrix}x+y=5\\x-y=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)

\(\Leftrightarrow\left(x^2+\dfrac{y^2}{4}+\dfrac{9}{4}+xy-3x-\dfrac{3y}{2}\right)+\dfrac{3}{4}\left(y^2-2y+1\right)=0\)

\(\Leftrightarrow\left(x+\dfrac{y}{2}-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\left(y-1\right)^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{y}{2}-\dfrac{3}{2}=0\\y-1=0\end{matrix}\right.\)

\(\Rightarrow x=y=1\)

<=> \(x^2+y^2+\left(xy-3x\right)-\left(3y-3\right)=0\)

\(\Leftrightarrow x^2+y^2+3x^2\left(y-1\right)-3\left(y-1\right)=0\)

<=> \(x^2+y^2\left(3x^2-3\right)\left(y-1\right)=0\)

\(\Leftrightarrow x^2+y^2.3.\left(x-1\right)\left(x+1\right)\left(y-1\right)=0\)

=> x = 0 ; 1 ; -1  . y =0  ; 1

P/s : ngủ được ròi:3

a, Cộng vế theo vế hai phương trình ta được:

\(x^2+y^2+2xy+x+y=2\)

\(\Leftrightarrow\left(x+y\right)^2+x+y-2=0\)

\(\Leftrightarrow\left(x+y-1\right)\left(x+y+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+y=1\\x+y=-2\end{matrix}\right.\)

TH1: \(x+y=1\)

\(pt\left(2\right)\Leftrightarrow xy+1=-1\Leftrightarrow xy=-2\)

Ta có hệ: \(\left\{{}\begin{matrix}x+y=1\\xy=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\xy=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\\\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\end{matrix}\right.\)

TH2: \(x+y=-2\)

\(pt\left(2\right)\Leftrightarrow xy-2=-1\Leftrightarrow xy=1\)

Ta có hệ: \(\left\{{}\begin{matrix}x+y=-2\\xy=1\end{matrix}\right.\Leftrightarrow x=y=-1\)

b, \(\left\{{}\begin{matrix}x^3-y^3=7\left(x-y\right)\\x^2+y^2=x+y+2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)\left(x^2+y^2+xy-7\right)=0\\x^2+y^2=x+y+2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=y\\x^2+y^2+xy=7\end{matrix}\right.\\x^2+y^2=x+y+2\end{matrix}\right.\)

TH1: \(\left\{{}\begin{matrix}x=y\\x^2+y^2=x+y+2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=y\\x^2-x-1=0\end{matrix}\right.\)

\(\Leftrightarrow x=y=\dfrac{1\pm\sqrt{5}}{2}\)

TH2: \(\left\{{}\begin{matrix}x^2+y^2+xy=7\\x^2+y^2=x+y+2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2-xy=7\\\left(x+y\right)^2-2xy-x-y=2\end{matrix}\right.\)

Đặt \(x+y=u;xy=v\)

Hệ trở thành: \(\left\{{}\begin{matrix}u^2-v=7\\u^2-2v-u=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}v=u^2-7\\u^2-2\left(u^2-7\right)-u=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}v=u^2-7\\u^2+u-12=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}v=u^2-7\\\left[{}\begin{matrix}u=3\\u=-4\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}v=2\\u=3\end{matrix}\right.\\\left\{{}\begin{matrix}v=9\\u=-4\end{matrix}\right.\end{matrix}\right.\)

Với \(\left\{{}\begin{matrix}v=2\\u=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}xy=2\\x+y=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\end{matrix}\right.\)

Với \(\left\{{}\begin{matrix}v=9\\u=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}xy=9\\x+y=-4\end{matrix}\right.\left(vn\right)\)

a.

ĐKXĐ: \(1\le x\le7\)

\(\Leftrightarrow x-1-2\sqrt{x-1}+2\sqrt{7-x}-\sqrt{\left(x-1\right)\left(7-x\right)}=0\)

\(\Leftrightarrow\sqrt{x-1}\left(\sqrt{x-1}-2\right)-\sqrt{7-x}\left(\sqrt{x-1}-2\right)=0\)

\(\Leftrightarrow\left(\sqrt{x-1}-\sqrt{7-x}\right)\left(\sqrt{x-1}-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}=\sqrt{7-x}\\\sqrt{x-1}=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=7-x\\x-1=4\end{matrix}\right.\)

\(\Leftrightarrow...\)

b. ĐKXĐ: ...

Biến đổi pt đầu:

\(x\left(y-1\right)-\left(y-1\right)^2=\sqrt{y-1}-\sqrt{x}\)

Đặt \(\left\{{}\begin{matrix}\sqrt{x}=a\ge0\\\sqrt{y-1}=b\ge0\end{matrix}\right.\)

\(\Rightarrow a^2b^2-b^4=b-a\)

\(\Leftrightarrow b^2\left(a+b\right)\left(a-b\right)+a-b=0\)

\(\Leftrightarrow\left(a-b\right)\left(b^2\left(a+b\right)+1\right)=0\)

\(\Leftrightarrow a=b\)

\(\Leftrightarrow\sqrt{x}=\sqrt{y-1}\Rightarrow y=x+1\)

Thế vào pt dưới:

\(3\sqrt{5-x}+3\sqrt{5x-4}=2x+7\)

\(\Leftrightarrow3\left(x-\sqrt{5x-4}\right)+7-x-3\sqrt{5-x}=0\)

\(\Leftrightarrow\dfrac{3\left(x^2-5x+4\right)}{x+\sqrt{5x-4}}+\dfrac{x^2-5x+4}{7-x+3\sqrt{5-x}}=0\)

\(\Leftrightarrow\left(x^2-5x+4\right)\left(\dfrac{3}{x+\sqrt{5x-4}}+\dfrac{1}{7-x+3\sqrt{5-x}}\right)=0\)

\(\Leftrightarrow...\)