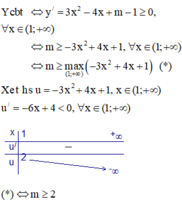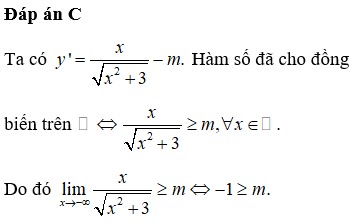tìm m để y = \(\frac{-1}{3}\)x3 + (m-1)x2+(m+3)x-4 đồng biến trên khoảng (0;3)

Những câu hỏi liên quan
Tìm m để hàm số
y
x
3
−
2
x
2
+
(
m
−
1
)
x
+
3
−
m
đồng biến trên khoảng
(
1
;
+
∞
)
.
A.
m
≤
3
B. m 3 C. m -1 D.
m
≥
2
Đọc tiếp
Tìm m để hàm số y = x 3 − 2 x 2 + ( m − 1 ) x + 3 − m đồng biến trên khoảng ( 1 ; + ∞ ) .
A. m ≤ 3
B. m > 3
C. m < -1
D. m ≥ 2
Tìm m để hàm số
y
x
3
-
2
x
2
+
(
m
-
1
)
x
+
3
-
m
đồng biến trên khoảng
1
;
+
∞
A.
m
≤
3
B. m3 C. m -1 D.
m
≥
2
Đọc tiếp
Tìm m để hàm số y = x 3 - 2 x 2 + ( m - 1 ) x + 3 - m đồng biến trên khoảng 1 ; + ∞
A. m ≤ 3
B. m>3
C. m < -1
D. m ≥ 2
Tìm m để hàm số
y
(
m
2
-
m
-
3
)
x
3
+
3
(
m
-
1
)
x
2
-
3
x
đồng biến trên
-
∞
;
+
∞
Đọc tiếp
Tìm m để hàm số y = ( m 2 - m - 3 ) x 3 + 3 ( m - 1 ) x 2 - 3 x đồng biến trên - ∞ ; + ∞
![]()
![]()
Tìm giá trị của tham số m để các hàm số y
x
3
- 2m
x
2
+ 12x - 7 đồng biến trên R.A. m 4 B. m
∈
(0;
∞
)C. m
∈
(-
∞
; 0) D. -3
≤
m
≤
3
Đọc tiếp
Tìm giá trị của tham số m để các hàm số y = x 3 - 2m x 2 + 12x - 7 đồng biến trên R.
A. m = 4 B. m ∈ (0; ∞ )
C. m ∈ (- ∞ ; 0) D. -3 ≤ m ≤ 3
Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3 x 2 - 4mx + 12 ≥ 0, ∀ x ⇔ ∆ ' = 4m2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.
Đúng 0
Bình luận (0)
Tìm giá trị của tham số m để các hàm số y = x 3 - 2m x 2 + 12x - 7 đồng biến trên R.
A. m = 4 B. m ∈ (0; ∞ )
C. m ∈ ( - ∞ ; 0) D. -3 ≤ m ≤ 3
Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3 x 2 - 4mx + 12 ≥ 0, ∀x ⇔ Δ' = 4 m 2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.
Đúng 0
Bình luận (0)
Tìm m để hàm số
y
x
3
+
m
x
2
+
1
−
2
m
x
+
m
−
3
đồng biến trên khoảng (-3;0) A.
m
≥
2
3
+
3
B.
m
≤
2
3
−...
Đọc tiếp
Tìm m để hàm số y = x 3 + m x 2 + 1 − 2 m x + m − 3 đồng biến trên khoảng (-3;0)
A. m ≥ 2 3 + 3
B. m ≤ 2 3 − 3
C. m ≤ 6 + 42
D. m ≥ 6 − 42
Đáp án B
Ta có y ' = 3 x 2 + 2 m x + 1 − 2 m
Hàm số đồng biến trên − 3 ; 0 ⇔ y ' ≥ 0 , ∀ x ∈ − 3 ; 0 ⇔ 3 x 2 + 2 m x + 1 − 2 m ≥ 0 , ∀ x ∈ − 3 ; 0
⇔ m 2 x − 2 ≥ − 3 x 2 − 1 ⇔ m ≤ − 3 x 2 + 1 2 x − 2 , x ∈ − 3 ; 0 1
Xét hàm số
f x = − 3 x 2 + 1 2 x − 2 , x ∈ − 3 ; 0 ⇒ f ' x = − 6 x 2 + 12 x + 2 2 x − 2 2 ⇒ f ' x = 0 ⇔ x = 3 ± 2 3 3
Ta có bảng biến thiên hàm số f x như sau:
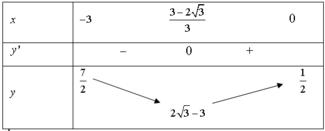
Suy ra f x − 3 ; 0 ≥ 2 3 − 3 ⇒ 1 ⇔ m ≤ 2 3 − 3
Đúng 0
Bình luận (0)
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y
x
3
-
(
m
+
1
)
x
2
+
3
x
+
1
đồng biến trên khoảng từ
(
-
∞
;
+
∞
)
A.
(
-
∞
;
-
4
)
∪
(
2...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = x 3 - ( m + 1 ) x 2 + 3 x + 1 đồng biến trên khoảng từ ( - ∞ ; + ∞ )
A. ( - ∞ ; - 4 ) ∪ ( 2 ; + ∞ )
B. [-4;2]
C. ( - ∞ ; - 4 ] ∪ [ 2 ; + ∞ )
D. (-4;2)
Với giá trị nào của m thì hàm số
y
x
3
+
(
m
+
1
)
x
2
-
(
3
m
+
2
)
x
+
4
đồng biến trên khoảng
(
0
;
1
)
A.
m
≤
-
2
3
B.
m
≥
-
2
3...
Đọc tiếp
Với giá trị nào của m thì hàm số y = x 3 + ( m + 1 ) x 2 - ( 3 m + 2 ) x + 4 đồng biến trên khoảng ( 0 ; 1 )
A. m ≤ - 2 3
B. m ≥ - 2 3
C. m ≤ 3
D. m ≥ 3
Đáp án C
Ta có: y’ = 3x2 + 2(m+1)x – (3m+2)
Hàm số đồng biến trên khoảng (0;1)
3x2 + 2(m+1)x – (3m+2) ≥ 0 ∀ x ∈ (0;1)
⇔ m ≤ − 3 x 2 + 2 x − 2 2 x − 3 ∀ x ∈ (0;1)
Xét hàm số: g = − 3 x 2 + 2 x − 2 2 x − 3 D =(0;1)
Ta có: g’ = − 6 x 2 − 18 x − 2 ( 2 x − 3 ) 2
ð g’ = 0 ⇔ x = 9 ± 93 6 (không thoản mãn)
Ta có bảng biến thiên
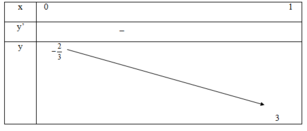
Vậy với m ≤ 3 hàm số đồng biến trên khoảng (0;1)
Đúng 0
Bình luận (0)
Tìm tập hợp tất cả các giá trị của tham số m để hàm số
y
x
2
+
3
-
m
(
x
+
1
)
đồng biến trên khoảng
(
-
∞
;
+
∞
)
A.
[
1
;
+
∞
)
B.
[
-
1
;
...
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số m để hàm số y = x 2 + 3 - m ( x + 1 ) đồng biến trên khoảng ( - ∞ ; + ∞ )
A. [ 1 ; + ∞ )
B. [ - 1 ; 1 ]
C. ( - ∞ ; - 1 ]
D. ( - ∞ ; 1 )