

Những câu hỏi liên quan
Giúp em câu cuối ạ 
giúp em câu cuối với ạ

Giúp em hai câu cuối với ạ !!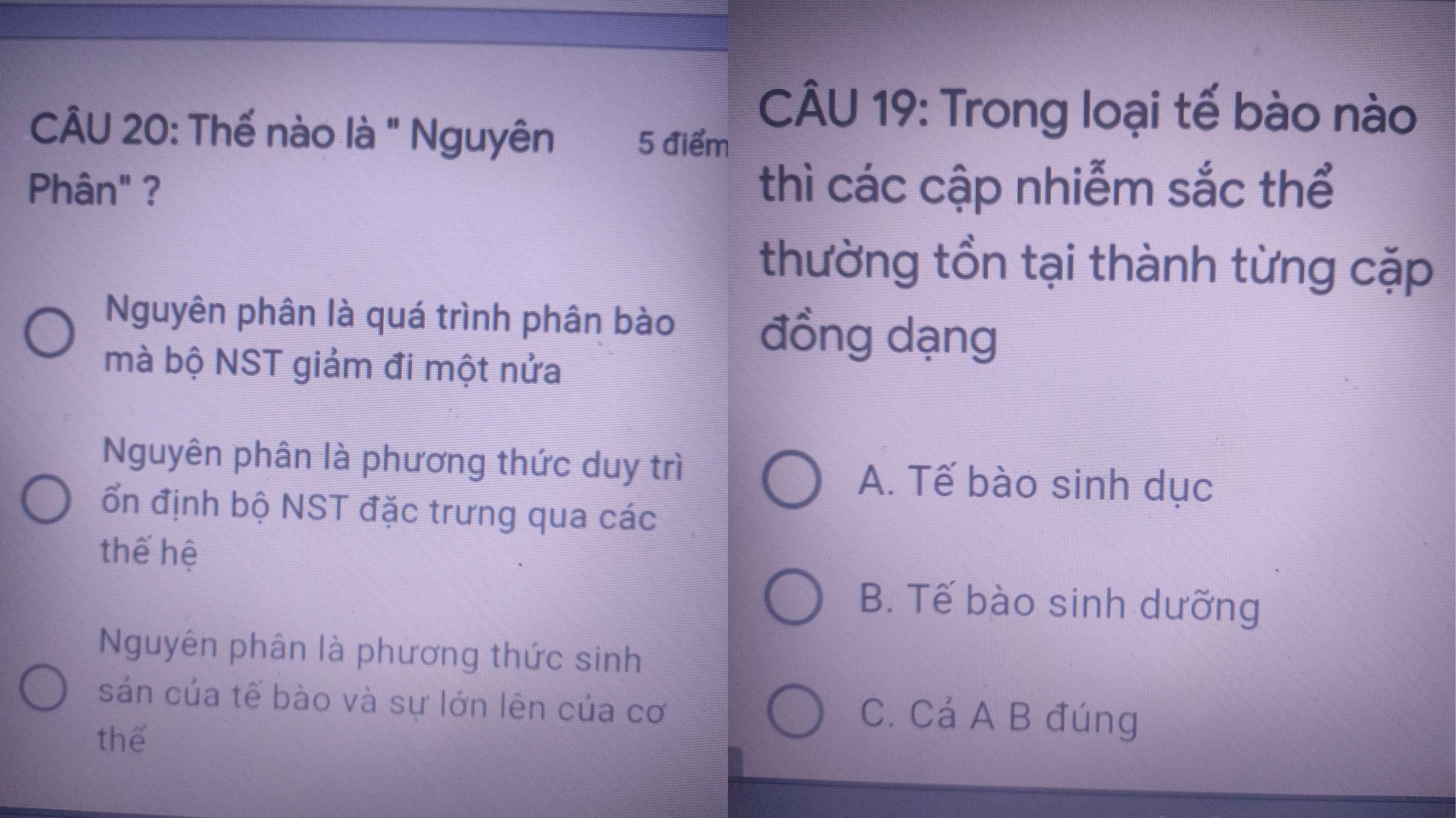
19B (tế bào sinh dục gồm: tb sinh dục sơ khai có bộ NST tồn tại thành từng cặp tương đồng; giao tử có bộ NST tồn tại thành từng chiếc đơn lẻ)
20C
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
2 câu cuối ạ giúp em với 
giúp em 2 câu cuối gấp ạ!!!
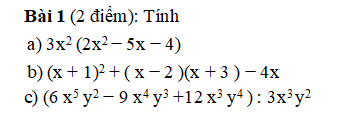
\(a,=6x^5-15x^3-12x^2\\ b,=x^2+2x+1+x^2+x-6-4x=2x^2-x-5\\ c,=2x^2-3xy+4y^2\)
Đúng 2
Bình luận (0)
Giải giúp em 4 câu cuối với ạ
Em cảm ơn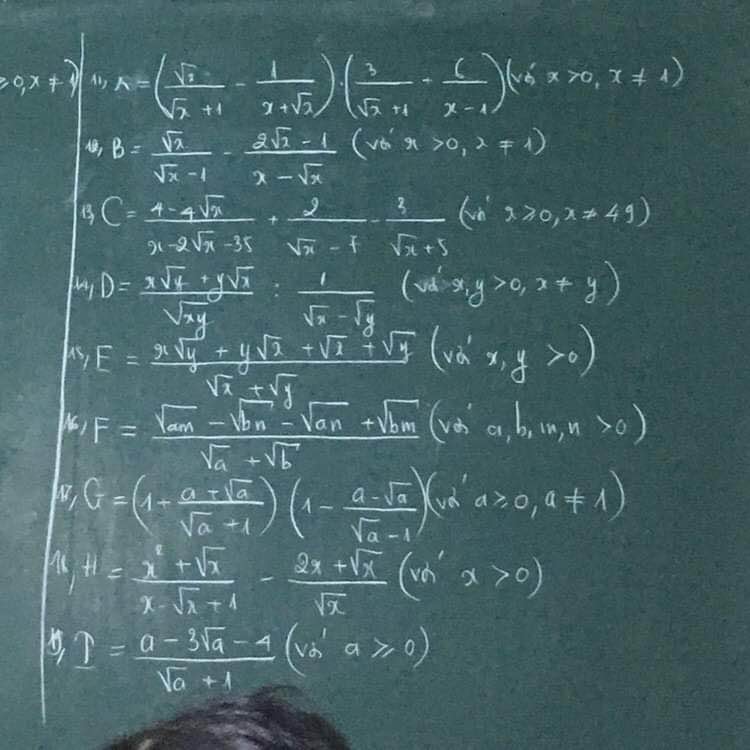
18) Ta có: \(H=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(=\sqrt{x}\cdot\left(\sqrt{x}+1\right)-\left(2\sqrt{x}-1\right)\)
\(=x+\sqrt{x}-2\sqrt{x}+1\)
\(=x-\sqrt{x}+1\)
19) Ta có: \(T=\dfrac{a-3\sqrt{a}-4}{\sqrt{a}+1}\)
\(=\dfrac{\left(\sqrt{a}-4\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\sqrt{a}-4\)
Đúng 1
Bình luận (1)
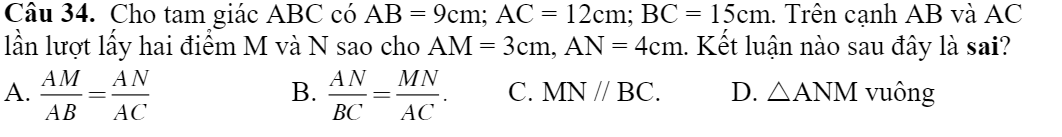
Giúp em câu cuối này được ko ạ?
Đừng làm tắt ạ không hiểu
Làm giúp em 4 câu cuối này ạ
a: \(\sqrt{252}+\dfrac{1}{3}\sqrt{63}-\sqrt{175}\)
\(=4\sqrt{7}+\sqrt{7}-5\sqrt{7}\)
=0
Đúng 0
Bình luận (0)
giúp em hai câu e,f cuối với ạ 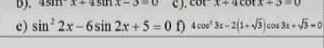
e) \(sin^22x-6sin2x+5=0\Rightarrow\) \(\left[{}\begin{matrix}sin2x=5\left(loại\right)\\sin2x=1\end{matrix}\right.\)
\(\Rightarrow sin2x=sin\left(\dfrac{\pi}{2}\right)\)
\(\Rightarrow2x=\dfrac{\pi}{2}+k2\pi\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
f.
\(4cos^23x-2\left(\sqrt{3}+1\right)cos3x+\sqrt{3}=0\)
\(\Leftrightarrow4cos^23x-2cos3x-2\sqrt{3}cos3x+\sqrt{3}=0\)
\(\Leftrightarrow2cos3x\left(2cos3x-1\right)-\sqrt{3}\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left(2cos3x-\sqrt{3}\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\\cos3x=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
























