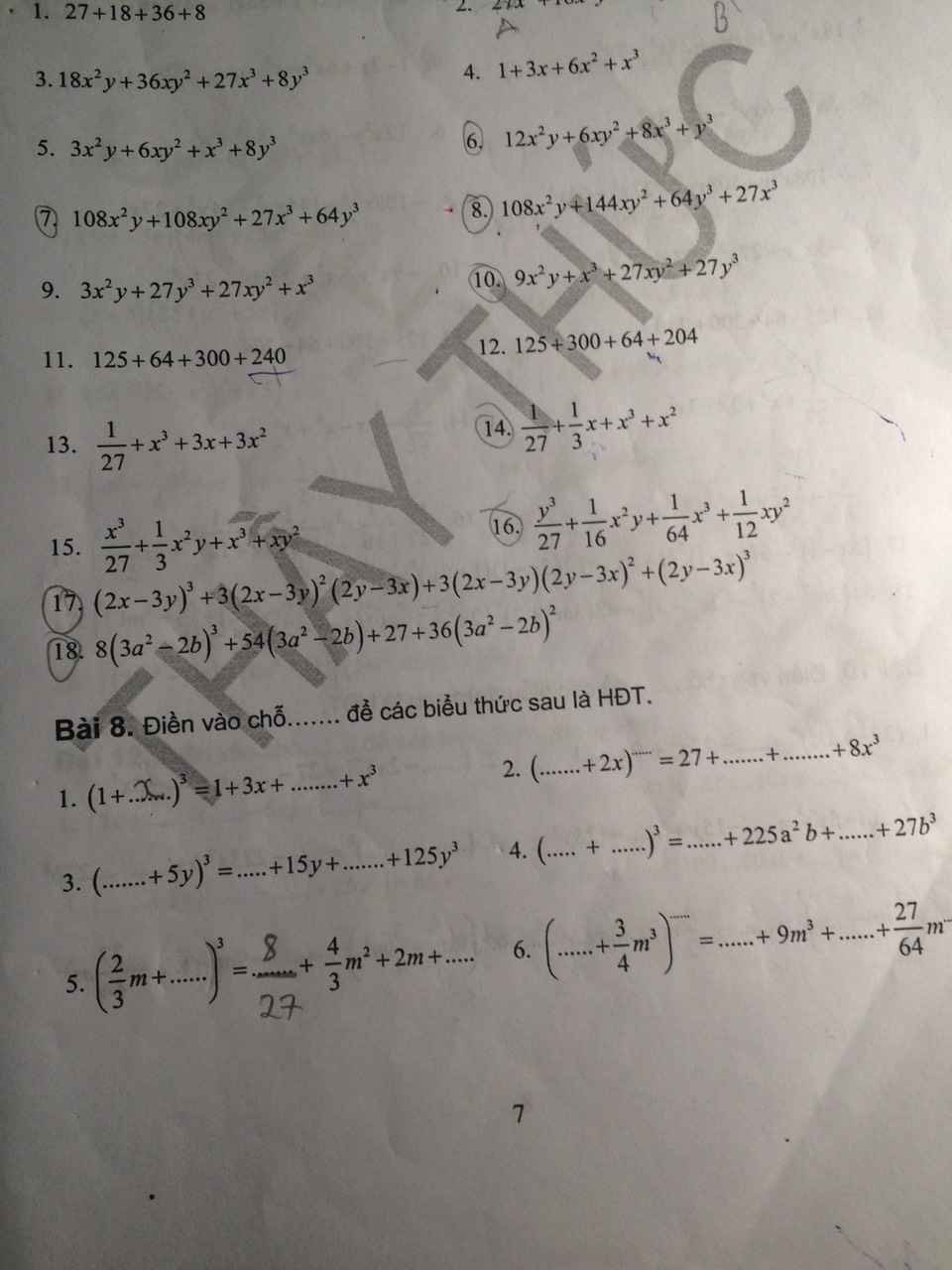
6) Ta có: \(12x^2y+6xy^2+8x^3+y^3\)

\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2+y^3\)

\(=\left(2x+y\right)^3\)

8) Ta có: \(108x^2y+144xy^2+64y^3+27x^3\)

\(=\left(4y\right)^3+3\cdot\left(4y\right)^2\cdot3x+3\cdot4y\cdot\left(3x\right)^2+\left(3x\right)^3\)

\(=\left(4y+3x\right)^3\)

nhân chéo lên

nhân a+b+c từ 9/a+b+c sang vế trái

vế phải còn 9

sau đó nhân vế trái ra 

sử dụng bdt cosi là ra nha bn

mik lớp 7 sory

 1/a + 1/b + 1/c ≥ 9/(a+b+c)
<=> (1/a + 1/b + 1/c )(a+b+c) ≥ 9
Ta có : 1/a + 1/b + 1/c ≥ 3.căn bậc 3 1/abc
a+b+c ≥ 3 căn bậc 3 abc
(1/a + 1/b + 1/c)(a+c+c) ≥ 9 căn bậc 3 abc/abc = 9
<=> 1/a + 1/b + 1/c ≥ 9(a+b+c)
Dấu ''='' xảy ra khi : a=b =c

Trong toán học, một bất đẳng thức là một phát biểu về quan hệ thứ tự giữa hai đối tượng.

·         Ký hiệu  a<b  có nghĩa là a nhỏ hơn b và

·         Ký hiệu  a > b có nghĩa là a lớn hơn b.

Những quan hệ nói trên được gọi là bất đẳng thức nghiêm ngặt; ngoài ra ta còn cócác bất đẳng thức không ngặt :

·  có nghĩa là a nhỏ hơn hoặc bằng b và

·   có nghĩa là a lớn hơn hoặc bằng b.

Người ta còn dùng một ký hiệu khác để chỉ ra rằng một đại lượng lớn hơn rất nhiều so với một đại lượng khác.

Ký hiệu a >> b có nghĩa là a lớn hơn b rất nhiều.

Các ký hiệu a, b ở hai vế của một bất đẳng thức có thể là các biểu thức của các biến. Sau đây ta chỉ xét các bất đẳng thức với các biến nhận giá trị trên tập số thực hoặc các tập con của nó.

Nếu một bất đẳng thức đúng với mọi giá trị của tất cả các biến có mặt trong bất đẳng thức, thì bất đẳng thức này được gọi là bất đẳng thức tuyệt đối hay không điều kiện. Nếu một bất đẳng thức chỉ đúng với một số giá trị nào đó của các biến, với các giá trị khác thì nó bị đổi chiều hay không còn đúng nữa thì nó được goị là một bất đẳng thức có điều kiện. Một bất đẳng thức đúng vẫn còn đúng nếu cả hai vế của nó được thêm vào hoặc bớt đi cùng một giá trị, hay nếu cả hai vế của nó được nhân hay chia với cùng một số dương. Một bất đẳng thức sẽ bị đảo chiều nếu cả hai vế của nó được nhân hay chia bởi một số âm.

Hai bài toán thường gặp trên các bất đẳng thức là

1.   Chứng minh bất đẳng thức đúng với trị giá trị của các biến thuộc một tập hợp cho trước, đó là bài toán chứng minh bất đẳng thức.

2.   Tìm tập các giá trị của các biến để bất đẳng thức đúng. Đó là bài toán giải bất phương trình.

3.   Tìm giá trị lớn nhất,nhỏ nhất của một biểu thức một hay nhiều biến.

Dài quá bạn viết mình chẳng hiểu

*mik~ viết~ đại ~zậy~ hoy *

pn cố gắng trích ra nhé :)))

Chúc pn hok giỏi nhoaa!!!!!!!

Bài làm:

Ta có: \(A=x+\frac{1}{x^2}=\left(\frac{1}{x^2}+\frac{x}{8}+\frac{x}{8}\right)+\frac{3}{4}x\ge3\sqrt[3]{\frac{1}{x^2}.\frac{x}{8}.\frac{x}{8}}+\frac{3}{4}.2\)

\(=3.\frac{1}{4}+\frac{3}{2}=\frac{3}{4}+\frac{3}{2}=\frac{9}{4}\)

Dấu "=" xảy ra khi: \(\frac{1}{x^2}=\frac{x}{8}\Leftrightarrow x^3=8\Leftrightarrow x=2\)

Vậy \(Min\left(A\right)=\frac{9}{4}\)khi \(x=2\)

Học tốt!!!!

\(\frac{2016.\left(2016+1\right)}{2016}=2017\)

Vậy có 2017 đường  thẳng