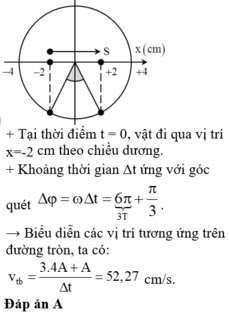
Vật dao động điều hòa theo phương trình : x=4cos(20t−2π/3) (cm). Tốc độ vật sau khi đi quảng đường S = 2 (cm) (kể từ lúc t = 0) là
A. 20 (cm/s)
B. 60 (cm/s)
C. 80 (cm/s)
D. 40 (cm/s)

Những câu hỏi liên quan
Một vật dao động điều hòa theo phương trình
x
4
cos
(
20
t
-
2
π
3
)
(cm; s). Vận tốc trung bình của vật sau khoảng thời gian
t
19
π
60
s kể từ khi bắt đầu dao động là A. 52,27 cm/s. B. 50,71 cm/s. C. 50,28 cm/s. D. 54,31 cm/s.
Đọc tiếp
Một vật dao động điều hòa theo phương trình x = 4 cos ( 20 t - 2 π 3 ) (cm; s). Vận tốc trung bình của vật sau khoảng thời gian t = 19 π 60 s kể từ khi bắt đầu dao động là
A. 52,27 cm/s.
B. 50,71 cm/s.
C. 50,28 cm/s.
D. 54,31 cm/s.
Một vật dao động điều hòa với phương trình: x=4cos(4\(\pi\)t + \(\pi\)/4)(cm), t tính bằng giây(s). Quảng đường vật đi được sau 0,25 s kể từ khi bắt đầu chuyển động là
Để tính quãng đường vật đi được sau 0,25 s, ta có thể sử dụng phương trình dao động điều hòa x = A * cos(2π/T * t + φ), trong đó x là vị trí của vật (cm), A là biên độ của vật (cm), T là chu kỳ của dao động (s), t là thời gian (s), và φ là góc pha ban đầu (rad).
Trong trường hợp này, phương trình dao động là x = 4cos(4πt + π/4). Ta có thể nhận thấy rằng biên độ của vật là 4 cm và chu kỳ của dao động là T = 1/4 s.
Để tính quãng đường vật đi được sau 0,25 s, ta thay t = 0,25 vào phương trình:
x = 4cos(4π * 0,25 + π/4)
x = 4cos(π + π/4)
x = 4cos(5π/4)
x ≈ 4 * (-0,7071)
x ≈ -2,8284 cm
Vậy, quãng đường vật đi được sau 0,25 s kể từ khi bắt đầu chuyển động là khoảng -2,8284 cm.
Đúng 0
Bình luận (0)
Một vật dao động điều hòa có phương trình x = 5cos(2πt – π/6) cm. Lấy π2 = 10. Vận tốc của vật khi t = 3(s) là
A. -5π (cm/s).
B. 5π (cm/s).
C. -2,5√3(cm/s).
D. 2,5√3(cm/s).
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Rightarrow v=...\)
Đúng 0
Bình luận (0)
Một vật dao động điều hòa theo phương ngang có tốc độ góc rad/s. Lúc vật ở vị trí 3 cm thì truyền cho nó vận tốc 20 cm/s. Chọn gốc thời gian lúc vật ở vị trí 2,5 và theo chiều dương. Lập phương trình dao động.
A. x=5cos(5πt + π/4) (cm)
B. x=4cos(5πt + π/4) (cm)
C. x=5cos(5πt - π/4) (cm)
D. x=4cos(5πt - π/4) (cm)
Chọn gốc thời gian lúc vật ở vị trí 2,5√2 (em ghi sai chổ đó)
Đúng 0
Bình luận (0)
Một vật dao động điều hòa theo phương trình x = 10cos(πt + π/3 ) (cm/s). Kể từ lúc t = 0 thời điểm vận tốc của vật có độ lớn 5π (cm/s) lần thứ 21 là:
Trong `5` chu kì vật đi qua thời điểm vận tốc có độ lớn `5\pi(cm//s)` là `20` lần.
`=>1` lần vật đi trong: `\Delta t=T/12+T/6=T/4`
`=>` Kể từ `t=0` thời điểm vận tốc của vật có độ lớn `5\pi(cm//s)` lần thứ `21` là:
`t=T/4+5T=10,5(s)`.
Đúng 0
Bình luận (0)
Một vật dao động điều hòa với tần số góc 20 rad/s trên đoạn thăng AB=8(cm) Chọn gốc tọa độ ở vị trí cân bằng, chiều dương từ A đến B, gốc thời gian lúc vật ở B. Phương trình dao động của vật làA. x=4 cos(20t+ pi 2 )(cm) B. x=8 cos(20t- pi 2 )(cm) .C. x=8 cos(20t+ pi 2 )(cm) .D. x=4cos 20t(cm)
Một chất điểm dao động điều hòa theo phương trình x = 4cos(2π/3)t, (x tính bằng cm, t tính bằng s). Kể từ t = 0, chất điểm đi qua vị trí có li độ x = -2 cm lần thứ 2019 tại thời điểm
A. 6030 s.
B. 3028 s.
C. 3015 s.
D. 3016 s.
Đáp án B
Chu kì dao động của chất điểm 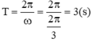
Ta có hình vẽ
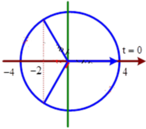
Một chu kì vật đi qua vị trí x = - 2 cm hai lần. Từ hình vẽ ta thấy, để vật đi qua vị trí x = -2 cm lần thứ 2019 cần thời gian 1009T + T/3 = 3028s
Đúng 0
Bình luận (0)
Một vật dao động điều hòa với phương trình x = 4cos(2pi*t - pi/3) cm. Tốc độ trung bình cực tiểu mà vật đạt dduocj trong khảng thời gian 2/3 chu kì dao động là
A. 18,92 cm/s
B. 18 cm/s
C. 13,6 cm/s
D. 15,51 cm/s
Tốc độ trung bình = quãng đường đi được trong thời gian t chia cho thời gian đi.
\(v=\frac{s}{t}.\)
v min khi s min.
s min khi quãng đường đi được ứng với một cung tròn \(\widehat{aNb}\) lấy biên làm trung điểm. Như hình tròn ở dưới. (Nếu S max thì quãng đường đi được ứng với cung tròn lấy vị trí cân bằng làm trung điểm)
\(t=\frac{T}{6}\Rightarrow\widehat{aNb}=t.\omega=\frac{2T}{3}.\frac{2\pi}{T}=\frac{4\pi}{3}>\pi.\)
\(S_{min}=s_1\left(\pi\right)+s_{2min}\left(\frac{\pi}{3}\right)\)Do cung lớn hơn 180 độ ta tách \(\pi+\frac{\pi}{3}.\)
\(s_1\left(\pi\right)=2A.\) là quãng đường đi được ứng với cung 180 độ.
Tính quãng đường nhỏ nhất đi được ứng với cung 60 độ \(s_{2min}\left(\frac{\pi}{3}\right)\)
=> \(\varphi=\frac{\frac{\pi}{3}}{2}=\frac{\pi}{6}.\)
Tương ứng với cung tròn \(aNb\) là \(s_{2min}=2.MN=2.\left(A-A\cos\varphi\right)=2A\left(1-\cos\varphi\right).\)
\(s_{min}=s_1+s_2=2A+2A\left(1-\cos30\right)=9,07cm.\)
vận tốc trung bình là \(v=\frac{s}{t}=\frac{9,07}{\frac{2T}{3}}=13,6\)cm/s.
Đúng 0
Bình luận (0)
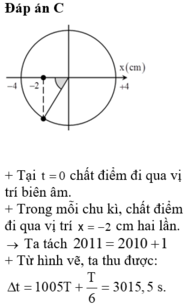
Một chất điểm dao động điều hòa theo phương trình x 4cos(2π/3 + π) (x tính bằng cm; t tính bằng s). Kể từ t 0, chất điểm đi qua vị trí có li độ x -2 cm lần thứ 2011 tại thời điểm A. 3016,5 s. B. 6030,5 s. C. 3015,5 s. D. 6031,5 s.
Đọc tiếp
Một chất điểm dao động điều hòa theo phương trình x = 4cos(2π/3 + π) (x tính bằng cm; t tính bằng s). Kể từ t = 0, chất điểm đi qua vị trí có li độ x = -2 cm lần thứ 2011 tại thời điểm
A. 3016,5 s.
B. 6030,5 s.
C. 3015,5 s.
D. 6031,5 s.