Chứng minh trong HCN giới hạn bởi các đt :
X=5,5
X=41
Y=2
Y=17
không có điểm nguyên nào thuộc đường thẳng 3x+5y=7
(mn giúp mk vs )
chứng minh rằng trong hình chữ nhật giới hạn bởi các đường thẳng x=5,5; x=41; y=2 ; y=17 ; không có điểm nguyên nào thuộc đường thẳng 3x+5y=7
CMR hình chữ nhật giới hạn bởi các đường thẳng
x=6; x=42 ; y=2; y=17 không có điểm có tọa độ nguyên nào thuộc đường thẳng 3x+5y=7
Xét hàm số y = f(x) liên tục trên miền D = [a;b] có đồ thị là một đường cong C. Gọi S là phần giới hạn bởi C và các đường thẳng x = a; x = b Người ta chứng minh được rằng độ dài đường cong S bằng ∫ a b 1 + ( f ' ( x ) ) 2 d x Theo kết quả trên, độ dài đường cong S là phần đồ thị của hàm số f(x) = ln x và bị giới hạn bởi các đường thẳng x = 1 ; x = 3 là m - m + ln 1 + m n với m , n ∈ R thì giá trị của m 2 - m n + n 2 là bao nhiêu?
A. 6
B. 7
C. 3
D. 1
Diện tích hình phẳng giới hạn bởi các đường y = x và x - 2y = 0 bằng với diện tích của hình nào trong các hình dưới đây?
A. Hình vuông có cạnh bằng 2
B. Hình chữ nhật có chiều dài, chiều rộng lần lượt là 5 và 3.
C. Hình tròn có bán kính bằng 3
D. Diện tích toàn phần khối tứ diện đều có cạnh bằng 2 3 3
Phương trình hoành độ giao điểm của hai đường y = x và x - 2 y = 0 ⇔ y = x 2 là x = x 2 ⇔ x ≥ 0 x = x 2 4 ⇔ x = 0 hoặc x = 4
Diện tích hình phẳng cần tìm là
S ∫ 0 4 x - x 2 d x = ∫ 0 4 x - x 2 d x = 2 x 3 3 - x 2 4 0 4 = 4 3
Diện tích toàn phần của một khối tứ diện đều cạnh 2 3 4 3 là S x q = 4 . 2 3 4 3 2 3 4 = 4 3
Đáp án D
Tính diện tích của hình phẳng giới hạn bởi các đường sau: y = 2 x 2 + x – 6 và 2y = - x 2 + 3x + 6
Miền cần tính diện tích được thể hiện bởi Hình 9 (học sinh tự làm)
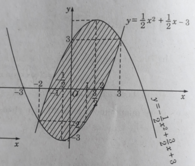
Như vậy, với mọi x ∈ (-2;3) đồ thị của hàm số
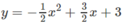
nằm phía trên đồ thị của hàm số
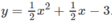
Vậy ta có:
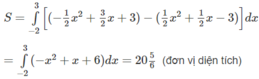
Diện tích hình phẳng được giới hạn bởi các đường y = x 3 + 3 x , y = - x và đường thẳng x = -2 là:
A. -12(dvdt).
B. 12(dvdt).
C. 4(dvdt).\
D. -4(dvdt).
Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = x3 + 3x và y = -x là: x3 + 4x = 0 ⇔ x = 0
Ta có: x3 + 4x ≤ 0, ∀ x ∈ [-2;0].
Do đó:
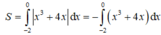
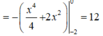
Từ 1 điểm A nằm bên ngoài đường tròn tâm O bán kính 2cm kẻ 2 tiep tuyến AM,AN tới đường tròn.
1, Chứng minh tứ giác AMON nội tiếp được 1 đường tròn.
2,kẻ đường kính NOB,chứng minh BM//AO.
3,Gọi I là giao điểm của MN với AO. chứng minh MO×NI=AN×OI
4,Tính ₫ộ dài cung nhỏ MN của đường tròn tâm O và diện tích hình quạt tròn giới hạn bởi các đoạn thẳng OM,ON và cung nhỏ MN nếu góc MON =120°.
Mọi người giúp mình với nha.mai thi rồi.làm ơn giúp mình với,cam ơn a
cho tam giác abc vuông tại a đường cao ah. d là trung điểm ab, e là trung điểm ah, f là giao của đường trung trực của ab với ce.f(-1;3) pt bc:x-2y+1=0. biết d thuộc đt 3x+5y+0 và hoành độ nguyên tìm a,b,c
Tìm trên trục hoành các điểm có hoành độ là số nguyên sao cho nếu qua điểm đó ta dựng đường thẳng vuông góc với trục hoành thì đường thẳng ấy cắt cả ba đường thẳng (d1):x-2y=3 , (d2):x-3y=2 , (d3):x-5y= -7 tại các điểm có tọa độ là các số nguyên
Gọi các điểm thỏa mãn điều kiện có tọa độ là \(\left(a;0\right)\)
Khi đó hệ sau có nghiệm nguyên:\(\hept{\begin{cases}a-2y=3\\a-3y=2\\x-5y=-7\end{cases}\Rightarrow\frac{a-3}{2};\frac{a-2}{3};\frac{a+7}{5}}\) nguyên.
TH1: \(a\ge0.\)
\(\frac{a-3}{2}\in Z\) nên a lẻ; \(\frac{a+7}{5}\in Z\Rightarrow\) a chia 5 dư 3. Kết hợp hai điều kiện trên thì a có tận cùng là 3.
Khi đó a - 2 có tận cùng là 1. Vậy để \(\frac{a-2}{3}\in Z\) thì a - 2 = 34k \(\left(k\in N;k\ge1\right)\)
Vậy a = 2 +34k \(\left(k\in N;k\ge1\right)\)
TH2: a < 0
\(\frac{a-3}{2}\in Z\Rightarrow\)- a là số tự nhiên lẻ. \(\frac{a+7}{5}\in Z\Rightarrow\) -a chia 5 dư 2. Vậy -a có tận cùng là 7, vậy a có tận cùng là 7.
Vậy thì a - 2 có tận cùng là 9. Vậy a - 2 = -34k+2 \(\left(k\in N;k\ge0\right)\)
Hay a = 2 - 34k+2 \(\left(k\in N;k\ge0\right)\)
Tóm lại các điểm thỏa mãn điều kiện của đề bài sẽ có tọa độ là \(\left(2+3^{4k};0\right)\) với \(\left(k\in N;k\ge1\right)\) hoặc \(\left(2-3^{4k+2};0\right)\) với \(\left(k\in N;k\ge0\right)\)