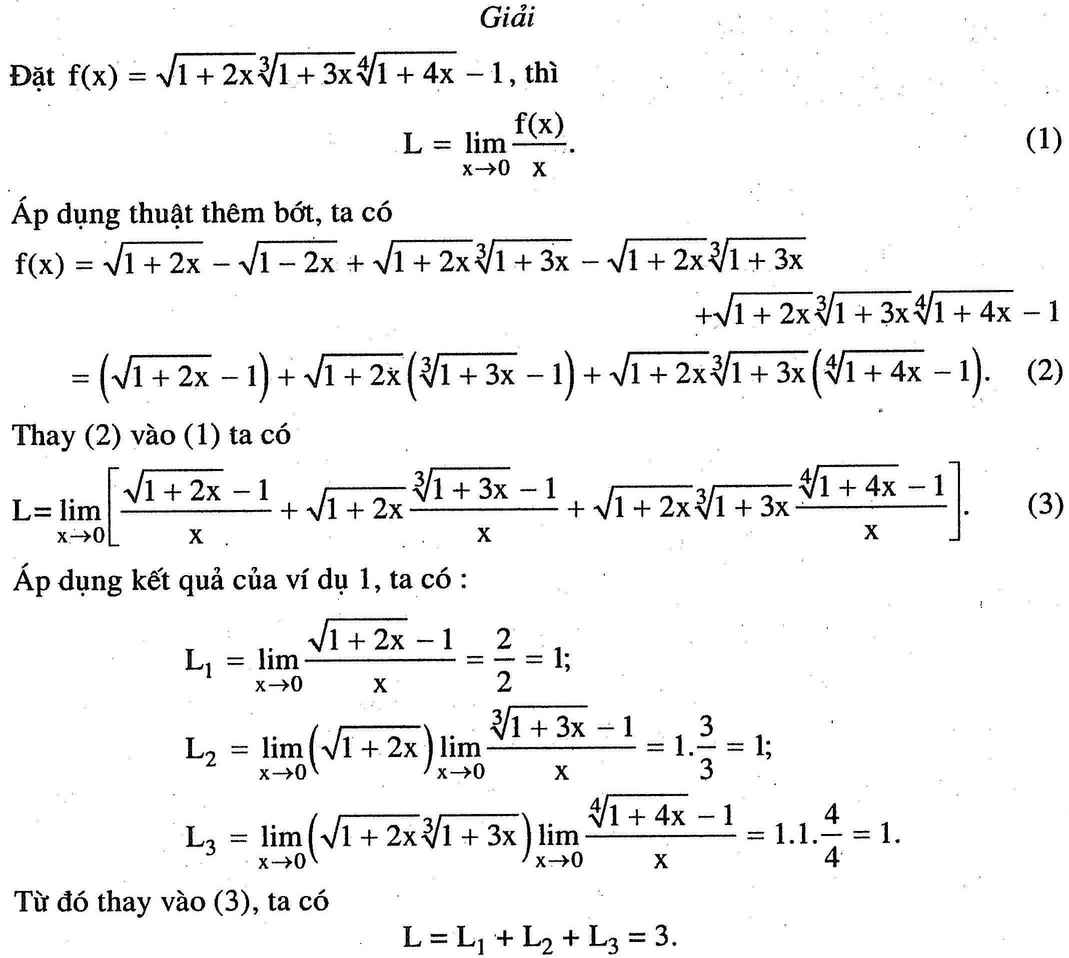Bài 1:

\(a=\lim\limits_{x\rightarrow+\infty}\frac{\frac{1}{x}+\frac{2}{\sqrt{x}}-1}{1+\frac{3}{x}}=-1\)

\(b=\lim\limits_{x\rightarrow+\infty}\frac{1+\frac{3}{x^2}-\frac{1}{x^3}}{\frac{1}{\sqrt{x}}+\frac{1}{x^2}}=\frac{1}{0}=+\infty\)

\(c=\lim\limits_{x\rightarrow-\infty}\frac{1-2\sqrt{\frac{1}{x^2}-\frac{1}{x}}}{\frac{1}{x}-1}=\frac{1}{-1}=-1\)

Bài 2:

\(a=\lim\limits_{x\rightarrow0}\frac{1-cosx}{1-cos3x}=\lim\limits_{x\rightarrow0}\frac{sinx}{3sin3x}=\lim\limits_{x\rightarrow0}\frac{\frac{sinx}{x}}{9.\frac{sin3x}{3x}}=\frac{1}{9}\)

\(b=\lim\limits_{x\rightarrow0}\frac{cotx-sinx}{x^3}=\frac{\infty}{0}=+\infty\)

\(c=\lim\limits_{x\rightarrow\infty}\frac{sinx}{2x}\)

Mà \(\left|sinx\right|\le1\Rightarrow\left|\frac{sinx}{2x}\right|\le\frac{1}{\left|2x\right|}\)

Mà \(\lim\limits_{x\rightarrow\infty}\frac{1}{2\left|x\right|}=0\Rightarrow\lim\limits_{x\rightarrow\infty}\frac{sinx}{2x}=0\)

\(A=\lim\limits_{x\rightarrow0}\frac{\left(x+1\right)^{\frac{1}{3}}-1}{\left(2x+1\right)^{\frac{1}{4}}-1}=\lim\limits_{x\rightarrow0}\frac{\frac{1}{3}\left(x+1\right)^{-\frac{2}{3}}}{\frac{1}{2}\left(2x+1\right)^{-\frac{3}{4}}}=\frac{\frac{1}{3}}{\frac{1}{2}}=\frac{2}{3}\)

\(B=\lim\limits_{x\rightarrow7}\frac{\sqrt[3]{4x-1}\sqrt{x-2}}{\sqrt[4]{2x+2}-2}=\frac{3\sqrt{5}}{0}=+\infty\)

\(C=\lim\limits_{x\rightarrow0}\frac{\sqrt{\left(3x+1\right)\left(4x+1\right)}\left(\sqrt{2x+1}-1\right)}{x}+\lim\limits_{x\rightarrow0}\frac{\sqrt{4x+1}\left(\sqrt{3x+1}-1\right)}{x}+\lim\limits_{x\rightarrow0}\frac{\sqrt{4x+1}-1}{x}\)

Xét \(\lim\limits_{x\rightarrow0}\frac{\sqrt{ax+1}-1}{x}=\lim\limits_{x\rightarrow0}\frac{\left(ax+1\right)^{\frac{1}{2}}-1}{x}=\lim\limits_{x\rightarrow0}\frac{\frac{a}{2}\left(ax+1\right)^{-\frac{1}{2}}}{1}=\frac{a}{2}\)

\(\Rightarrow C=\frac{2}{2}+\frac{3}{2}+\frac{4}{2}=\frac{9}{2}\)

\(D=\lim\limits_{x\rightarrow0}\frac{\left(1+4x\right)^{\frac{1}{2}}-\left(1+6x\right)^{\frac{1}{3}}}{x^2}=\lim\limits_{x\rightarrow0}\frac{2\left(1+4x\right)^{-\frac{1}{2}}-2\left(1+6x\right)^{-\frac{2}{3}}}{2x}\)

\(D=\lim\limits_{x\rightarrow0}\frac{-2\left(1+4x\right)^{-\frac{3}{2}}+4\left(1+6x\right)^{-\frac{5}{3}}}{1}=-2+4=2\)

\(E=\lim\limits_{x\rightarrow0}\frac{\left(1+ax\right)^{\frac{1}{n}}-\left(1+bx\right)^{\frac{1}{n}}}{x}=\lim\limits_{x\rightarrow0}\frac{\frac{a}{n}\left(1+ax\right)^{\frac{1-n}{n}}-\frac{b}{n}\left(1+bx\right)^{\frac{1-n}{n}}}{1}=\frac{a-b}{n}\)

\(B=\lim\limits_{x\rightarrow7}\frac{\sqrt[3]{4x-1}-\sqrt{x+2}}{\sqrt[4]{2x+2}-2}=\lim\limits_{x\rightarrow7}\frac{\left(4x-1\right)^{\frac{1}{3}}-\left(x+2\right)^{\frac{1}{2}}}{\left(2x+2\right)^{\frac{1}{4}}-2}\)

\(B=\lim\limits_{x\rightarrow7}\frac{\frac{4}{3}\left(4x-1\right)^{-\frac{2}{3}}-\frac{1}{2}\left(x+2\right)^{-\frac{1}{2}}}{\frac{1}{2}\left(2x+2\right)^{-\frac{3}{4}}}=\lim\limits_{x\rightarrow7}\frac{\frac{4}{3\sqrt[3]{\left(4x-1\right)^2}}-\frac{1}{2\sqrt{x+2}}}{\frac{1}{2}\sqrt[4]{\left(2x+2\right)^3}}\)

\(=\frac{\frac{4}{3\sqrt[3]{27^2}}-\frac{1}{2\sqrt{9}}}{\frac{1}{2}\sqrt[4]{16^3}}=-\frac{1}{216}\)

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x^2+1}-\left(x+1\right)}{2x^2-x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt{x^2+1}-\left(x+1\right)\right)\left(\sqrt{x^2+1}+x+1\right)}{x\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{-2x}{x\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{-2}{\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)

\(=\dfrac{-2}{\left(0-1\right)\left(\sqrt{1}+1\right)}=1\)

a. \(\lim\limits_{x\rightarrow2}\dfrac{x-2}{x^2-4}=\lim\limits_{x\rightarrow2}\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\lim\limits_{x\rightarrow2}\dfrac{1}{x+2}=\dfrac{1}{4}\)

b. \(\lim\limits_{x\rightarrow3^-}\dfrac{x+3}{x-3}=\lim\limits_{x\rightarrow3^-}\dfrac{-x-3}{3-x}\)

Do \(\lim\limits_{x\rightarrow3^-}\left(-x-3\right)=-6< 0\)

\(\lim\limits_{x\rightarrow3^-}\left(3-x\right)=0\) và \(3-x>0;\forall x< 3\)

\(\Rightarrow\lim\limits_{x\rightarrow3^-}\dfrac{-x-3}{3-x}=-\infty\)

Ta xét:

\(\sqrt{1+2x}\cdot\sqrt[3]{1+3x}-1\)

\(=\sqrt{1+2x}-\sqrt{1+2x}+\sqrt{1+2x}\cdot\sqrt[3]{1+2x}-1\)

\(=\left(\sqrt{1+2x}-1\right)+\sqrt{1+2x}\cdot\left(\sqrt[3]{1+2x}-1\right)\)

Xét giới hạn trên:

\(\Rightarrow^{lim}_{x\rightarrow0}\dfrac{\sqrt{1+2x}\cdot\sqrt[3]{1+2x}-1}{x}\)

   \(=^{lim}_{x\rightarrow0}\left(\dfrac{\sqrt{1+2x}-1}{x}\right)+^{lim}_{x\rightarrow0}\left(\dfrac{\sqrt{1+2x}\cdot\left(\sqrt[3]{1+2x}-1\right)}{3}\right)\)

Tính giới hạn từng thành phần:

* \(^{lim}_{x\rightarrow0}\left(\dfrac{\sqrt{1+2x}-1}{x}\right)=^{lim}_{x\rightarrow0}\left(\dfrac{1+2x-1}{x\left(\sqrt{1+2x}+1\right)}\right)\)

  \(=^{lim}_{x\rightarrow0}\left(\dfrac{2}{\sqrt{1+2x}+1}\right)=\dfrac{2}{\sqrt{1+2\cdot0}+1}=1\left(1\right)\)

* \(^{lim}_{x\rightarrow0}\left(\dfrac{\sqrt{1+2x}\cdot\sqrt[3]{1+2x}-1}{x}\right)\)

  \(=^{lim}_{x\rightarrow0}\left(\sqrt{1+2x}\cdot\dfrac{1+2x-1}{x\left(\left(\sqrt[3]{1+2x}\right)^2+\sqrt[3]{1+2x}+1\right)}\right)\)

  \(=^{lim}_{x\rightarrow0}\left(\sqrt{1+2x}\cdot\dfrac{2}{\left(\sqrt[3]{1+2x}\right)^2+\sqrt[3]{1+2x}+1}\right)\)

  \(=\sqrt{1+2\cdot0}\cdot\dfrac{2}{(\sqrt[3]{1+2\cdot0})^2+\sqrt[3]{1+2\cdot0}+1}\)

  \(=\dfrac{2}{3}\left(2\right)\)

Lấy \(\left(1\right)+\left(2\right)\) ta được:

\(^{lim}_{x\rightarrow0}\dfrac{\sqrt{1+2x}\cdot\sqrt[3]{1+2x}-1}{x}=1+\dfrac{2}{3}=\dfrac{5}{3}\)

\(a=\lim\limits_{x\rightarrow-3}\frac{x^2+2x-3}{x\left(x+3\right)\left(x-\sqrt{3-2x}\right)}=\lim\limits_{x\rightarrow-3}\frac{\left(x-1\right)\left(x+3\right)}{x\left(x+3\right)\left(x-\sqrt{3-2x}\right)}=\lim\limits_{x\rightarrow-3}\frac{x-1}{x\left(x-\sqrt{3-2x}\right)}=-\frac{2}{9}\)

\(b=\lim\limits_{x\rightarrow0}\frac{\sqrt{x+9}-3+\sqrt{x+16}-4}{x}=\lim\limits_{x\rightarrow0}\frac{\frac{x}{\sqrt{x+9}+3}+\frac{x}{\sqrt{x+16}+4}}{x}=\lim\limits_{x\rightarrow0}\left(\frac{1}{\sqrt{x+9}+3}+\frac{1}{\sqrt{x+16}+4}\right)=\frac{7}{24}\)

\(c=\lim\limits_{x\rightarrow\frac{1}{2}}\frac{8x^2-1}{6x^2-5x+1}\) ko phải dạng vô định, đề bài là \(8x^2\) hay \(8x^3\) bạn?

\(d=\lim\limits_{x\rightarrow0}\frac{\left(\sqrt{x^2+1}-1\right)\left(\sqrt{x^2+1}+1\right)\left(4+\sqrt{x^2+16}\right)}{\left(4-\sqrt{x^2+16}\right)\left(4+\sqrt{x^2+16}\right)\left(\sqrt{x^2+1}+1\right)}\)

\(=\lim\limits_{x\rightarrow0}\frac{x^2\left(4+\sqrt{x^2+16}\right)}{-x^2\left(\sqrt{x^2+1}+1\right)}=\lim\limits_{x\rightarrow0}\frac{4+\sqrt{x^2+16}}{-\sqrt{x^2+1}-1}=\frac{8}{-2}=-4\)

Tất cả đều ko phải dạng vô định, bạn cứ thay số vào tính thôi:

\(a=\frac{sin\left(\frac{\pi}{4}\right)}{\frac{\pi}{2}}=\frac{\sqrt{2}}{\pi}\)

\(b=\frac{\sqrt[3]{3.4-4}-\sqrt{6-2}}{3}=\frac{0}{3}=0\)

\(c=0.sin\frac{1}{2}=0\)

a) \(\lim\limits_{x\rightarrow0}\frac{\sqrt{1+2x}-1}{2x}=\lim\limits_{x\rightarrow0}\frac{2x}{2x\left(\sqrt{1+2x}+1\right)}=\lim\limits_{x\rightarrow0}\frac{1}{\sqrt{1+2x}+1}=\frac{1}{2}\)

b) \(\lim\limits_{x\rightarrow0}\frac{4x}{\sqrt{9+x}-3}=\lim\limits_{x\rightarrow0}\frac{4x\left(\sqrt{9+x}+3\right)}{x}=\lim\limits_{x\rightarrow0}[4\left(\sqrt{9+x}+3\right)=24\)

c) \(\lim\limits_{x\rightarrow2}\frac{\sqrt{x+7}-3}{x-2}=\lim\limits_{x\rightarrow2}\frac{x-2}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=\lim\limits_{x\rightarrow2}\frac{1}{\sqrt{x+7}+3}=\frac{1}{6}\)

d) \(\lim\limits_{x\rightarrow1}\frac{3x-2-\sqrt{4x^2-x-2}}{x^2-3x+2}=\lim\limits_{x\rightarrow1}\frac{\left(3x-2\right)^2-\left(4x^2-4x-2\right)}{(x^2-3x+2)\left(3x-2+\sqrt{4x^2-x-2}\right)}=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(5x-6\right)}{\left(x-1\right)\left(x-2\right)\left(3x-2+\sqrt{4x^2-x-2}\right)}=\frac{1}{2}\\ \\\\ \\ \\ \\ \)

e)\(\lim\limits_{x\rightarrow1}\frac{\sqrt{2x+7}+x-4}{x^3-4x^2+3}=\lim\limits_{x\rightarrow1}\frac{2x+7-\left(x^2-8x+16\right)}{\left(x-1\right)\left(x^2-3x-3\right)\left(\sqrt{2x+7}-x+4\right)}=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x-9\right)}{\left(x-1\right)\left(x^2-3x-3\right)\left(\sqrt{2x+7}-x+4\right)}=\lim\limits_{x\rightarrow1}\frac{x-9}{\left(x^2-3x-3\right)\left(\sqrt{2x+7}-x+4\right)}=-8\)

f) \(\lim\limits_{x\rightarrow1}\frac{\sqrt{2x+7}-3}{2-\sqrt{x+3}}=\lim\limits_{x\rightarrow1}\frac{(2x-2)\left(2+\sqrt{x+3}\right)}{\left(1-x\right)\left(\sqrt{2x+7}+3\right)}=\lim\limits_{x\rightarrow1}\frac{-2\left(2+\sqrt{x+3}\right)}{\sqrt{2x+7}+3}=\frac{-4}{3}\)

g) \(\lim\limits_{x\rightarrow0}\frac{\sqrt{x^2+1}-1}{\sqrt{x^2+16}-4}=\lim\limits_{x\rightarrow0}\frac{x^2\left(\sqrt{x^2+16}+4\right)}{x^2\left(\sqrt{x^2+1}+1\right)}=4\)

h)

\(\lim\limits_{x\rightarrow4}\frac{\sqrt{x+5}-\sqrt{2x+1}}{x-4}=\lim\limits_{x\rightarrow4}\frac{\sqrt{x+5}-3}{x-4}+\lim\limits_{x\rightarrow4}\frac{3-\sqrt{2x+1}}{x-4}=\lim\limits_{x\rightarrow4}\frac{1}{\sqrt{x+5}+4}+\lim\limits_{x\rightarrow4}\frac{8-2x}{\left(x-4\right)\left(3+\sqrt{2x+1}\right)}=\frac{1}{7}-\frac{1}{3}=\frac{-4}{21}\)

k) \(\lim\limits_{x\rightarrow0}\frac{\sqrt{x+1}+\sqrt{x+4}-3}{x}=\lim\limits_{x\rightarrow0}\frac{\sqrt{x+1}-1}{x}+\lim\limits_{x\rightarrow0}\frac{\sqrt{x+4}-2}{x}=\lim\limits_{x\rightarrow0}\frac{1}{\sqrt{x+1}+1}+\lim\limits_{x\rightarrow0}\frac{1}{\sqrt{x+4}+2}=\frac{1}{2}+\frac{1}{4}=\frac{3}{4}\)

\(a=\frac{0-1}{0-1}=1\)

\(b=\lim\limits_{x\rightarrow0}\frac{\frac{x^2}{\sqrt[3]{\left(1+x^2\right)^2}+\sqrt[3]{1+x^2}+1}}{x^2}=\lim\limits_{x\rightarrow0}\frac{1}{\sqrt[3]{\left(1+x^2\right)^2}+\sqrt[3]{1+x^2}+1}=\frac{1}{3}\)

\(c=\lim\limits_{x\rightarrow2}\frac{\sqrt{x+2}-2+\sqrt{x+7}-3}{x-2}=\lim\limits_{x\rightarrow2}\frac{\frac{x-2}{\sqrt{x+2}+2}+\frac{x-2}{\sqrt{x+7}+3}}{x-2}=\lim\limits_{x\rightarrow2}\left(\frac{1}{\sqrt{x+2}+2}+\frac{1}{\sqrt{x+7}+3}\right)\)

\(=\frac{1}{\sqrt{4}+2}+\frac{1}{\sqrt{9}+3}=\frac{5}{12}\)